�O���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�������C�����悤�ɓ_P���ړ�����Ƃ��A�_P���ړ����邱�Ƃɂ���Ăł���}�`���O���Ƃ����B�O�Ղ́A����C�����_P�̏W���Ƃ������Ƃ��ł���B
��1�D�قȂ�2�_A�CB���瓙�����ɂ���_P�̋O�Ղ́AAB�̐��������B
��2�D��_C������̋���r�ɂ���_P�̋O�Ղ́AC�𒆐S�Ƃ��锼�ar�̉~�B
��3�D�قȂ�2�_A�CB�������ފp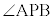 �����p�ł���_P�̋O�Ղ́AAB�a�Ƃ���~�B
�����p�ł���_P�̋O�Ղ́AAB�a�Ƃ���~�B
��4�D�قȂ�2�_A�CB�܂ł̋����̔䂪PA�FPB = m�Fn (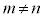 )�ň��ł���_P�̋O�Ղ́AAB��m�Fn�ɓ�������_��C�Cm�Fn�ɊO������_��D�Ƃ��āACD�a�Ƃ���~(�A�|���j�E�X�̉~�ƌĂ�Ă��܂��B�Ȃ��A���W���ʂɂ���������E�O�����Q��)�B
)�ň��ł���_P�̋O�Ղ́AAB��m�Fn�ɓ�������_��C�Cm�Fn�ɊO������_��D�Ƃ��āACD�a�Ƃ���~(�A�|���j�E�X�̉~�ƌĂ�Ă��܂��B�Ȃ��A���W���ʂɂ���������E�O�����Q��)�B
��5�D�قȂ�2��_ �C
�C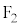 ����̋����̘a�����ł���_�̋O�Ղ́A
����̋����̘a�����ł���_�̋O�Ղ́A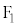 �C
�C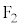 ���œ_�Ƃ���ȉ~�B
���œ_�Ƃ���ȉ~�B
��6�D�قȂ�2��_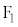 �C
�C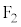 ����̋����̍������ł���_�̋O�Ղ́A
����̋����̍������ł���_�̋O�Ղ́A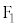 �C
�C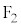 ���œ_�Ƃ���o�Ȑ��B
���œ_�Ƃ���o�Ȑ��B
��7�D��_F�܂ł̋����ƒ���l�܂ł̋������������_�̋O�Ղ́AF���œ_�A����l�������Ƃ���������B
���_P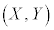 ��������������
��������������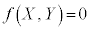 �ƁA�_P�C�_Q�̊W���w�肳��Ă��āAQ
�ƁA�_P�C�_Q�̊W���w�肳��Ă��āAQ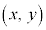 �̋O�Ղ����߂�ꍇ�́AX�CY�����ꂼ��
�̋O�Ղ����߂�ꍇ�́AX�CY�����ꂼ��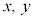 ��p���ĕ\���Ă����A
��p���ĕ\���Ă����A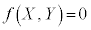 ��X�CY�̂Ƃ���ɑ������Ax�Cy�̊W��
��X�CY�̂Ƃ���ɑ������Ax�Cy�̊W��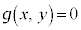 �������܂��B
�������܂��B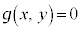 ���O�Ղ̕������ł��B
���O�Ղ̕������ł��B
(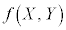 ��X�CY�̊W���A
��X�CY�̊W���A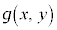 ��x�Cy�̊W���Ƃ����Ӗ��ł�)
��x�Cy�̊W���Ƃ����Ӗ��ł�)
x�Cy���}��ϐ���p���ĕ\����Ă���ꍇ�ɂ́A���̔}��ϐ�����������Ax�Cy�̊W��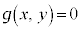 �������܂��B
�������܂��B
�O�Ղ����߂���ŁA�O�Ղ̕�����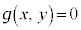 ������ꂽ�Ƃ��āA
������ꂽ�Ƃ��āA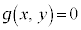 �����_�̂��ׂĂ���ӂ������ǂ������`�F�b�N����K�v������܂�(�^����ꂽ�����Ƌ��߂�ꂽ�O�Ղ��K�v�\�������ł��邱�Ƃ��m�F����K�v������̂ł��B�Ȃ��A�����E�������Q��)�B�������Ȃ��_������ꍇ�ɂ́A���O�_�ł��邱�Ƃ��ɕt�L���邱�ƁB
�����_�̂��ׂĂ���ӂ������ǂ������`�F�b�N����K�v������܂�(�^����ꂽ�����Ƌ��߂�ꂽ�O�Ղ��K�v�\�������ł��邱�Ƃ��m�F����K�v������̂ł��B�Ȃ��A�����E�������Q��)�B�������Ȃ��_������ꍇ�ɂ́A���O�_�ł��邱�Ƃ��ɕt�L���邱�ƁB
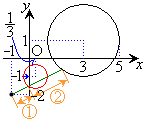
��8�D�~�F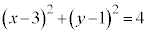 ��̓_P�Ɠ_A
��̓_P�Ɠ_A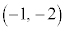 �����Ԑ�����2�F1�ɓ�������_Q�̋O��(���W���ʂɂ���������E�O�����Q��)�B
�����Ԑ�����2�F1�ɓ�������_Q�̋O��(���W���ʂɂ���������E�O�����Q��)�B
[��]�@P�CQ�̍��W��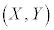 �C
�C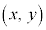 �Ƃ��āA
�Ƃ��āA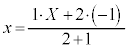 �C
�C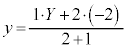
������A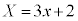 �C
�C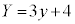 ����@
����@
X�CY�́A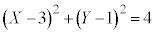 ��������A�@��������ƁA
��������A�@��������ƁA
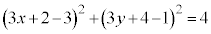
�� Q�̋O�Ղ́A�~�F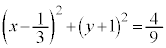 ......[��] (�}������ƉE�}�Ԑ�)
......[��] (�}������ƉE�}�Ԑ�)
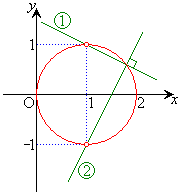 ��9�D�����F
��9�D�����F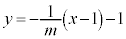 ����@�C�����F
����@�C�����F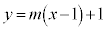 ����A �̌�_P�̋O��
����A �̌�_P�̋O��
[��]�@�������̎��͕�����ƁA
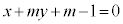 ����B
����B
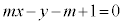 ����C
����C
�B�{�C�~m ���A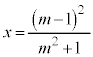 ����D�C�B�~m�|�C ���A
����D�C�B�~m�|�C ���A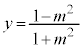 ����E
����E
�C���A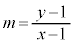 �ƕ\����邩��A������E�ɑ�������m���������邱�Ƃ��ł��܂��B
�ƕ\����邩��A������E�ɑ�������m���������邱�Ƃ��ł��܂��B

������Đ�������ƁA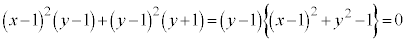
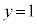 �̂Ƃ��E���
�̂Ƃ��E���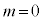 �ƂȂ邪�A���̂Ƃ������@�����݂��܂���B
�ƂȂ邪�A���̂Ƃ������@�����݂��܂���B
����āA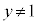 �ł����āA
�ł����āA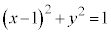 ����F
����F
�܂��A�E���A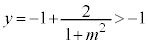 ���A
���A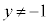 �ł��B
�ł��B
�F���� �Ƃ���ƁA
�Ƃ���ƁA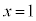
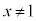 (
(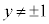 )���A�_
)���A�_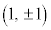 �͋O�ՂɊ܂܂�܂���B
�͋O�ՂɊ܂܂�܂���B
�ȏ���AP�̋O�Ղ́A�~�F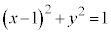 (�������A�_
(�������A�_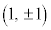 ������) ......[��] (�}������ƉE�}�Ԑ��A���}��������)
������) ......[��] (�}������ƉE�}�Ԑ��A���}��������)
[�ʉ�1]�@�@��A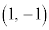 ��ʂ�X��
��ʂ�X��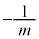 �̒����C�A��B
�̒����C�A��B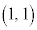 ��ʂ�X��m�̒���
��ʂ�X��m�̒���
�������̌X���̐ς�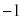 ������A�������͒������܂�(2�����̕��s�E�������Q��)�B
������A�������͒������܂�(2�����̕��s�E�������Q��)�B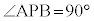 ������A�_P�̋O�Ղ́AAB�a�Ƃ���~�ɂȂ�܂��B�������A�@�͌X��0�̒�����\�����A�A�̌X��m��0�Ƃ���ƁA�����@�����݂��Ȃ��Ȃ邩��A�X��0�̒�����x���ɐ����Ȓ����Ƃ̌�_
������A�_P�̋O�Ղ́AAB�a�Ƃ���~�ɂȂ�܂��B�������A�@�͌X��0�̒�����\�����A�A�̌X��m��0�Ƃ���ƁA�����@�����݂��Ȃ��Ȃ邩��A�X��0�̒�����x���ɐ����Ȓ����Ƃ̌�_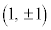 �͏�����܂��B
�͏�����܂��B
[�ʉ�2]�@�@���A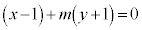 ����G�C�A���A
����G�C�A���A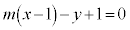 ����H
����H
�G�~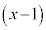 �|�H�~
�|�H�~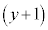 �Ƃ���m����������ƁA
�Ƃ���m����������ƁA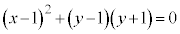
�� 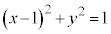 �C�O�Ղ̕����������߂邾���Ȃ炱�ꂪ��ԑ����B
�C�O�Ղ̕����������߂邾���Ȃ炱�ꂪ��ԑ����B
���O�_�̍l�@�͕ʉ�1�̂悤�ɍs���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 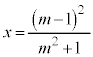 ����D�C�B�~m�|�C ���A
����D�C�B�~m�|�C ���A