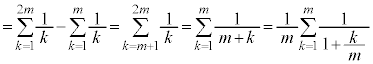��嗝�n���w'23�N�O��[1]
n��2�ȏ�̎��R���Ƃ���B
(1) 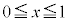 �̂Ƃ��A���̕s���������藧���Ƃ������B
�̂Ƃ��A���̕s���������藧���Ƃ������B (2) 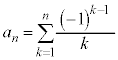 �Ƃ���Ƃ��A���̋Ɍ��l�����߂�B
�Ƃ���Ƃ��A���̋Ɍ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ɍ��l�̖��ł��B��㋉��(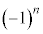 ���e���ɂ��Ă��āA�������e�����Ƃɓ���ւ��)�Ȃ̂ŁA���ɂ����͂���܂����A�͂��݂����̌`�������Ă���̂Ŗ��Ȃ��ł��傤�B
���e���ɂ��Ă��āA�������e�����Ƃɓ���ւ��)�Ȃ̂ŁA���ɂ����͂���܂����A�͂��݂����̌`�������Ă���̂Ŗ��Ȃ��ł��傤�B
(1) 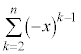 �́A�����F
�́A�����F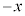 �C����F
�C����F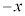 �C�����F
�C�����F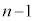 �����䐔���̘a�ł��B����āA
�����䐔���̘a�ł��B����āA �^�s�����̕s�����ɋ��܂ꂽ�����́A
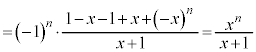 �@����@
�@����@����ŗ^�s�����́A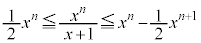 �Ɠ��l�ɂȂ�܂��B
�Ɠ��l�ɂȂ�܂��B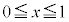 �Ȃ̂ŁA
�Ȃ̂ŁA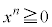 ���A
���A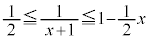 ��������悢���ƂɂȂ�܂�(�s�����̏ؖ����Q��)�B
��������悢���ƂɂȂ�܂�(�s�����̏ؖ����Q��)�B
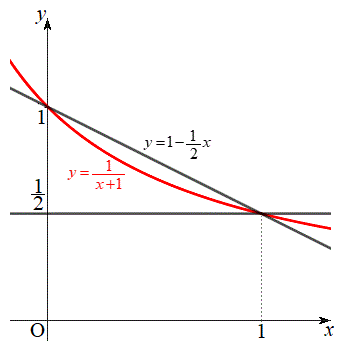 �E�}��`�������Ɋm�F�ł��܂����A
�E�}��`�������Ɋm�F�ł��܂����A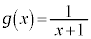 �Ƃ�������������ƁA
�Ƃ�������������ƁA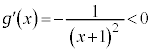 ���A
���A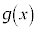 ��
��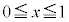 �ɂ������������ŁA
�ɂ������������ŁA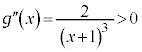 ���A
���A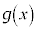 �̃O���t��
�̃O���t��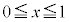 �ɂ����ĉ��ɓ�(���̉������Q��)�ł��B
�ɂ����ĉ��ɓ�(���̉������Q��)�ł��B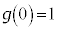 �C
�C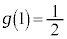 ���
���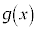 �̃O���t�́A2�_
�̃O���t�́A2�_ �C
�C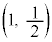 �����Ԓ���
�����Ԓ���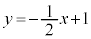 ���牺�ɂ���A����
���牺�ɂ���A����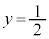 �����ɂ���܂��B����āA
�����ɂ���܂��B����āA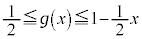 (�����@�̕s�����ւ̉��p(2)���Q��)�C�܂�A
(�����@�̕s�����ւ̉��p(2)���Q��)�C�܂�A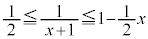 �C�e�ӂ�
�C�e�ӂ�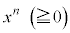 �������āA
�������āA �ƂȂ�A�@���A�^�s�������������܂��B
(2) (1)�̕s�����ɋ��܂ꂽ������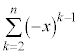 �ł����A���̂܂܂ł�
�ł����A���̂܂܂ł�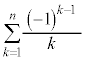 �Ɍ��т��Ȃ��̂ŁA
�Ɍ��т��Ȃ��̂ŁA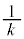 ����������o�����߂�(1)�̕s�����̊e�ӂ�
����������o�����߂�(1)�̕s�����̊e�ӂ�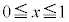 �͈̔͂Őϕ����܂�(��ϕ��ƕs�������Q��)�B
�͈̔͂Őϕ����܂�(��ϕ��ƕs�������Q��)�B 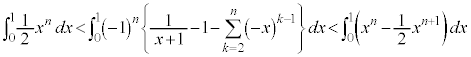 �@����A
�@����A�A���ӂ́A
�A�E�ӂ́A
����āA�A���A
�e�ӂ�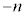 ��������ƁA
��������ƁA ���D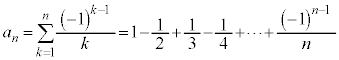 �ł����A
�ł����A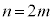 (m�F���R��)�̂Ƃ��A
(m�F���R��)�̂Ƃ��A �Ƃ����悤�ȍl�������m���Ă��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 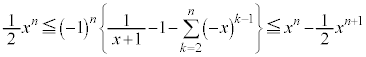
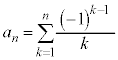 �Ƃ���Ƃ��A���̋Ɍ��l�����߂�B
�Ƃ���Ƃ��A���̋Ɍ��l�����߂�B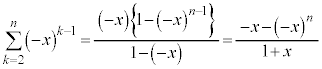
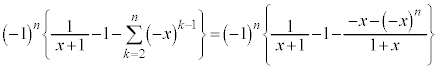
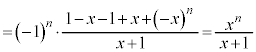 �@����@
�@����@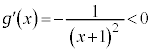 ���A
���A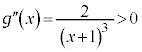 ���A
���A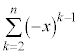 �ł����A���̂܂܂ł�
�ł����A���̂܂܂ł�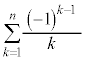 �Ɍ��т��Ȃ��̂ŁA
�Ɍ��т��Ȃ��̂ŁA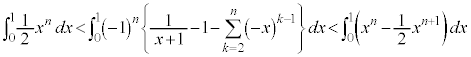 �@����A
�@����A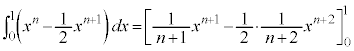
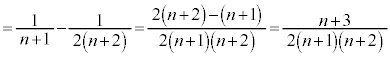
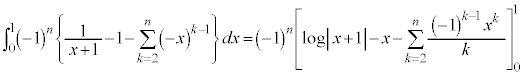
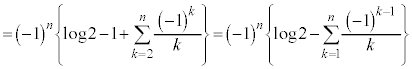
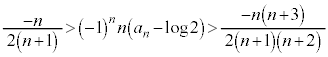
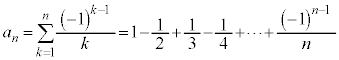 �ł����A
�ł����A