阪大理系数学'23年前期[3]
Pを座標平面上の点とし、点Pの座標を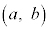 とする。
とする。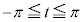 の範囲にある実数t のうち、曲線
の範囲にある実数t のうち、曲線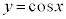 上の点
上の点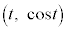 における接線が点Pを通るという条件をみたすものの個数を
における接線が点Pを通るという条件をみたすものの個数を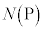 とする。
とする。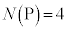 かつ
かつ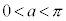 をみたすような点Pの存在範囲を座標平面上に図示せよ。
をみたすような点Pの存在範囲を座標平面上に図示せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 接線と領域の問題です。増減表を作ってから以降がややこしいですが、ていねいに場合分けして考えましょう。
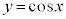 を微分すると、
を微分すると、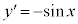
曲線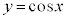 上の点
上の点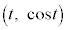 における接線は、
における接線は、
これが、点P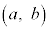 を通るので、
を通るので、
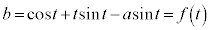 (
(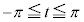 )とおくと、
)とおくと、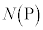 は、曲線
は、曲線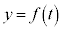 と直線
と直線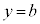 の
の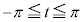 における共有点の数です(微分法の方程式への応用(2)を参照)。
における共有点の数です(微分法の方程式への応用(2)を参照)。
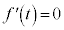 とすると、
とすると、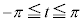 においては
においては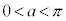 より、
より、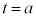 ,
,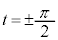
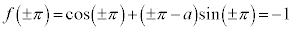 ,
,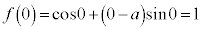 ,
,
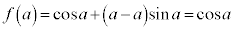 ,
,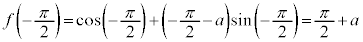 ,
,
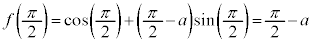
増減表より、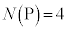 となることはありません。
となることはありません。 (ii) 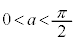 のとき、増減表は、
のとき、増減表は、 注.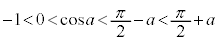 です。
です。 (iii) 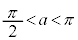 のとき、増減表は、
のとき、増減表は、 増減表より、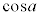 と
と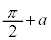 の大小関係、
の大小関係、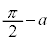 と
と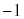 の大小関係が問題になりますが、
の大小関係が問題になりますが、
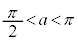 より
より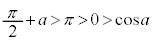 です。
です。
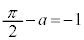 となるのは
となるのは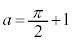 のときで、
のときで、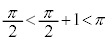 より、このとき
より、このとき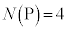 となるのは
となるのは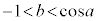 のときです。
のときです。 注.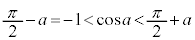 です。
です。 注.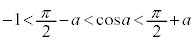 です。
です。 注.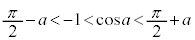 です。
です。 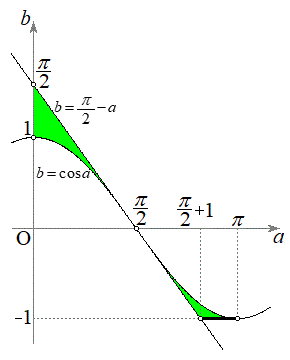 (i),(ii),(iii)をまとめて、
(i),(ii),(iii)をまとめて、 かつ
かつ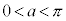 をみたすような点Pの存在範囲は、
をみたすような点Pの存在範囲は、
図示すると右図黄緑色着色部(直線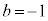 の
の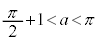 の太線部分を含み、他の境界線上の点、白マルを含まない)。
の太線部分を含み、他の境界線上の点、白マルを含まない)。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。