��嗝�n���w'23�N�O��[5]
1�̂��������n���āAk��ڂɏo���ڂ�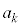 �Ƃ���B
�Ƃ���B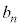 ��
��
�ɂ���`���A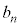 ��7�̔{���ƂȂ�m����
��7�̔{���ƂȂ�m����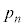 �Ƃ���B
�Ƃ���B
(1) 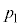 �C
�C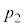 �����߂�B
�����߂�B (2) ����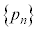 �̈�ʍ������߂�B
�̈�ʍ������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ǁA���������n��U���ďo���ڂ̘a��7�̔{���ƂȂ�m���A�Ɠ����Ȃ̂ł����A���Ɍ����Ă��܂��܂��B�Ȃ��A�����𐮐��Ŋ������Ƃ��̗]��ɂ��ẮA��]�����Q�Ƃ��Ă��������B
(1) ���������1����ƁA1����6�̖ڂ��o�܂����A�ǂ��7�Ŋ����Ȃ��̂ŁA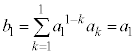 ��7�̔{���ƂȂ��m���́A
��7�̔{���ƂȂ��m���́A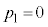 ......[��]
......[��] ���������2����ƁA
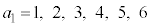 �̊e�X�ɂ��āA
�̊e�X�ɂ��āA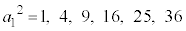 ��7�Ŋ������]��
��7�Ŋ������]��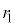 �́A
�́A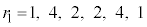 �ƂȂ�܂��B���̊e�X�ɂ��āA
�ƂȂ�܂��B���̊e�X�ɂ��āA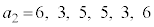 �ƂȂ�A
�ƂȂ�A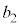 ��7�̔{���ɂȂ�܂��B
��7�̔{���ɂȂ�܂��B
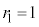 �C�܂�
�C�܂�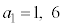 (�����Ȃ�m����
(�����Ȃ�m����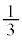 )�̂Ƃ��A
)�̂Ƃ��A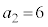 �ƂȂ�m����
�ƂȂ�m����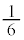 �ł��B
�ł��B
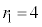 �C�܂�
�C�܂�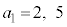 (�����Ȃ�m����
(�����Ȃ�m����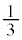 )�̂Ƃ��A
)�̂Ƃ��A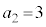 �ƂȂ�m����
�ƂȂ�m����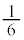 �ł��B
�ł��B
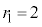 �C�܂�
�C�܂�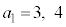 (�����Ȃ�m����
(�����Ȃ�m����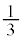 )�̂Ƃ��A
)�̂Ƃ��A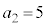 �ƂȂ�m����
�ƂȂ�m����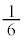 �ł��B
�ł��B
�����A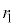 �C
�C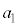 �����ł����Ă��A
�����ł����Ă��A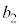 ��7�̔{���ƂȂ�悤��
��7�̔{���ƂȂ�悤��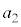 ���o��m����
���o��m����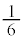 �ŁA������A
�ŁA������A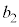 ��7�̔{���ƂȂ��m���́A
��7�̔{���ƂȂ��m���́A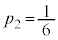 ......[��]
......[��]
(2) 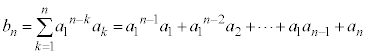 �ł����A
�ł����A 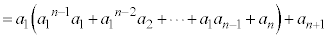
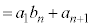 �@����@
�@����@����Ɋ�Â��āA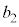 ����o������
����o������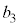 ���ǂ��Ȃ邩���l���Ă݂܂��B�@��
���ǂ��Ȃ邩���l���Ă݂܂��B�@��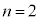 �Ƃ��āA
�Ƃ��āA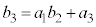 �ł��B
�ł��B
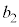 ��7�̔{���̂Ƃ�(�m��
��7�̔{���̂Ƃ�(�m��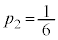 )�A
)�A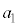 �����ł����Ă�
�����ł����Ă�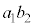 ��7�̔{���ł��B���̂Ƃ��A
��7�̔{���ł��B���̂Ƃ��A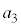 ��1�`6�̂ǂ�ł����Ă��A
��1�`6�̂ǂ�ł����Ă��A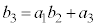 ��7�̔{���ɂ͂Ȃ�܂���B
��7�̔{���ɂ͂Ȃ�܂���B
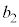 ��7�̔{���łȂ��Ƃ�(�m��
��7�̔{���łȂ��Ƃ�(�m��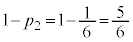 )�A�܂��A
)�A�܂��A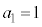 �̂Ƃ����l���Ă݂܂��B(1)�̌����ɂ���
�̂Ƃ����l���Ă݂܂��B(1)�̌����ɂ���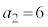 �̏ꍇ�ɂ�
�̏ꍇ�ɂ�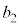 ��7�̔{���ł��B���̏ꍇ�ȊO�ɂ��āA
��7�̔{���ł��B���̏ꍇ�ȊO�ɂ��āA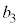 ��7�Ŋ������]����ȉ��̕\�Ɏ����܂��B�ȉ��̕\�ŁA
��7�Ŋ������]����ȉ��̕\�Ɏ����܂��B�ȉ��̕\�ŁA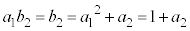 �ł��B
�ł��B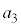 �̒l�ɑ���
�̒l�ɑ���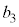 �̒l��
�̒l��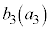 �̂悤�ɏ����܂��B�܂��A
�̂悤�ɏ����܂��B�܂��A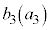 ��7�Ŋ������]���
��7�Ŋ������]���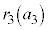 �̂悤�ɏ����܂��B
�̂悤�ɏ����܂��B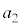 | 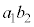 | 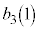 | 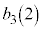 | 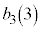 | 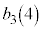 | 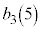 | 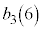 | 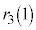 | 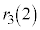 | 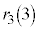 | 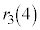 | 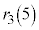 | 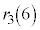 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 3 | 4 | 5 | 6 | 0 | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 4 | 5 | 6 | 0 | 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 5 | 6 | 0 | 1 | 2 | 3 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 6 | 0 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 0 | 1 | 2 | 3 | 4 | 5 |
�\���A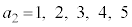 �̂�����̏ꍇ�ɂ��Ă��A����ɑΉ����āA
�̂�����̏ꍇ�ɂ��Ă��A����ɑΉ����āA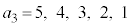 �ł����
�ł����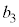 ��7�̔{���ɂȂ�܂��B
��7�̔{���ɂȂ�܂��B
�܂�A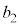 ��7�̔{���łȂ��ꍇ�A
��7�̔{���łȂ��ꍇ�A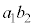 ��7�̔{���łȂ��A
��7�̔{���łȂ��A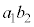 ��7�Ŋ������]���1�`6�̂ǂꂩ�ł���A���̂ǂ�ł������Ƃ��Ă��A
��7�Ŋ������]���1�`6�̂ǂꂩ�ł���A���̂ǂ�ł������Ƃ��Ă��A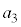 ��7���炻�̗]������������̖ڂł���A
��7���炻�̗]������������̖ڂł���A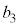 ��7�̔{���ɂȂ�܂��B
��7�̔{���ɂȂ�܂��B
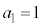 �ȊO�̏ꍇ(
�ȊO�̏ꍇ(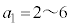 )�����l�ŁA
)�����l�ŁA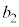 ��7�̔{���łȂ��Ȃ�
��7�̔{���łȂ��Ȃ�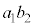 ��7�̔{���łȂ��A
��7�̔{���łȂ��A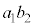 ��7�Ŋ������]���1�`6�̂ǂꂩ�ł���A���̂ǂ�ł������Ƃ��Ă��A
��7�Ŋ������]���1�`6�̂ǂꂩ�ł���A���̂ǂ�ł������Ƃ��Ă��A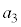 ��7���炻�̗]������������̖ڂł���A
��7���炻�̗]������������̖ڂł���A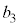 ��7�̔{���ɂȂ�܂��B
��7�̔{���ɂȂ�܂��B
�ȏ���܂Ƃ߂�ƁA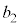 ��7�̔{���łȂ��ꍇ(�m��
��7�̔{���łȂ��ꍇ(�m��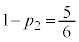 )�A
)�A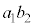 ��7�̔{���łȂ��A
��7�̔{���łȂ��A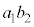 ��7�Ŋ������]���1�`6�̂ǂꂩ�ł���A���̂ǂ�ł������Ƃ��Ă��A
��7�Ŋ������]���1�`6�̂ǂꂩ�ł���A���̂ǂ�ł������Ƃ��Ă��A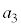 ��7���炻�̗]������������̖ڂł����(���̊m����
��7���炻�̗]������������̖ڂł����(���̊m����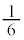 )�A
)�A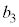 ��7�̔{���ɂȂ�܂��B
��7�̔{���ɂȂ�܂��B
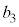 ��7�̔{���ɂȂ�m��
��7�̔{���ɂȂ�m��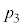 �́A
�́A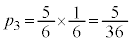 �ł��B
�ł��B
�@��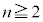 �̏ꍇ�����l�ɍl����ƁA
�̏ꍇ�����l�ɍl����ƁA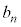 ��7�̔{���ł����
��7�̔{���ł����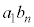 ��7�̔{���ł���A
��7�̔{���ł���A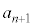 ��1�`6�̂ǂ�ł����Ă��A
��1�`6�̂ǂ�ł����Ă��A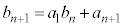 ��7�̔{���ɂȂ�܂���B
��7�̔{���ɂȂ�܂���B
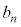 ��7�̔{���łȂ��Ƃ�(�m��
��7�̔{���łȂ��Ƃ�(�m��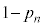 )�A
)�A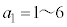 �̂�����ł����Ă�
�̂�����ł����Ă�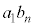 ��7�̔{���łȂ��A
��7�̔{���łȂ��A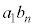 ��7�Ŋ������]���1�`6�̂ǂꂩ�ł���A���̂ǂ�ł������Ƃ��Ă��A
��7�Ŋ������]���1�`6�̂ǂꂩ�ł���A���̂ǂ�ł������Ƃ��Ă��A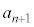 ��7���炻�̗]������������̖ڂł����(���̊m����
��7���炻�̗]������������̖ڂł����(���̊m����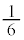 )�A
)�A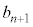 ��7�̔{���ɂȂ�܂�(���̊m����
��7�̔{���ɂȂ�܂�(���̊m����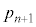 )�B����āA
)�B����āA 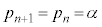 �Ƃ����ƁA
�Ƃ����ƁA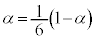 �@����B�@��
�@����B�@�� 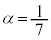
�A�|�B���A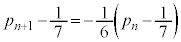
����́A����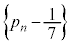 ���A����
���A����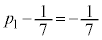 �C����
�C����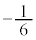 �����䐔���ł��邱�Ƃ��Ӗ����܂��B����āA
�����䐔���ł��邱�Ƃ��Ӗ����܂��B����āA 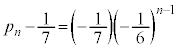 ��
�� 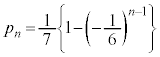 ......[��]
......[��]���D���̃J���N���������Ă��܂��A�{��́A�Q����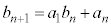 �ɂ����āA
�ɂ����āA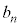 ��7�̔{���ł��邩�ǂ����A�Ƃ������ƂƁA
��7�̔{���ł��邩�ǂ����A�Ƃ������ƂƁA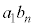 ��7�̔{���ł��邩�ǂ����A�Ƃ������Ƃ����l���Ƃ������Ƃ��~�\�ɂȂ��Ă����肾�Ƃ������Ƃ�������܂��B�܂�A�{��́An��ڂɏo���ڂ�
��7�̔{���ł��邩�ǂ����A�Ƃ������Ƃ����l���Ƃ������Ƃ��~�\�ɂȂ��Ă����肾�Ƃ������Ƃ�������܂��B�܂�A�{��́An��ڂɏo���ڂ�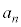 �Ƃ��āA
�Ƃ��āA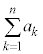 ��7�Ŋ�����m�������߂�A�Ƃ������Ɠ�����肾�Ƃ������Ƃł��B�ŏ����番�����Ă����J�͂Ȃ��킯�ł����A�o��҂́A���G�Ɍ����邽�߂ɁA
��7�Ŋ�����m�������߂�A�Ƃ������Ɠ�����肾�Ƃ������Ƃł��B�ŏ����番�����Ă����J�͂Ȃ��킯�ł����A�o��҂́A���G�Ɍ����邽�߂ɁA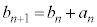 �Ƃ����A
�Ƃ����A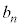 ��
��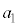 ��������
��������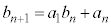 �Ƃ��ďo�肵���A�Ƃ������Ƃł��B
�Ƃ��ďo�肵���A�Ƃ������Ƃł��B 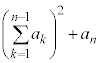 ��7�̔{���ƂȂ�m�������߂�A�Ƃ������ł������ł��B
��7�̔{���ƂȂ�m�������߂�A�Ƃ������ł������ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 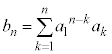
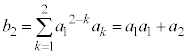
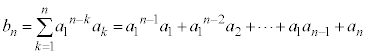 �ł����A
�ł����A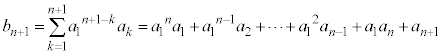
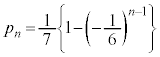 ......[��]
......[��]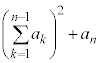 ��7�̔{���ƂȂ�m�������߂�A�Ƃ������ł������ł��B
��7�̔{���ƂȂ�m�������߂�A�Ƃ������ł������ł��B