�ꋴ�吔�w'05�N�O��[1]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
k�͐����ł���A3��������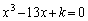 ��3�̈قȂ鐮���������Bk�Ƃ����̐����������ׂċ��߂�B
��3�̈قȂ鐮���������Bk�Ƃ����̐����������ׂċ��߂�B
���@�V���~�Ԃ��Œ��ׂčs���͈͂��A�����ɍi�邩�A�Ƃ������Ƃʼn����ł����������ł��B�Ȃ��A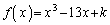 �̃O���t���l���Ă������Ƃ��ł��܂��B
�̃O���t���l���Ă������Ƃ��ł��܂��B
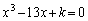 �@����@
�@����@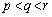 )�Ƃ���ƁA3���������̉��ƌW���̊W���A
)�Ƃ���ƁA3���������̉��ƌW���̊W���A
�A���A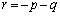
�B�ɑ������ƁA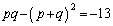
�������āA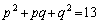
�����łǂ����邩�ł����A
���A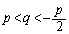 �@����D
�@����D
�Ȃ̂ŁA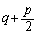 ���o�Ă���悤�ɕ����������A4�{����ƁA
���o�Ă���悤�ɕ����������A4�{����ƁA
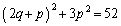 �@����E
�@����E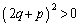 ���A
���A
�� 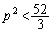
������݂����悤�Ȑ���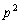 �́A
�́A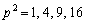 ��4�ʂ肵������܂���B
��4�ʂ肵������܂���B
�܂��A�A��D����l����ƁA3���̂����ł�������p��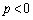 �ł��B
�ł��B
(i) 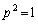 �C�܂�A
�C�܂�A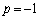 �̂Ƃ��A
�̂Ƃ��A �D���A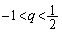
�����������q�́A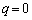
����́A�E�������s�K�B (ii) 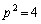 �C�܂�A
�C�܂�A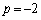 �̂Ƃ��A
�̂Ƃ��A �D���A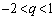
�����������q�́A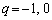
�ǂ�����E�������s�K�B (iii) 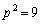 �C�܂�A
�C�܂�A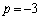 �̂Ƃ��A
�̂Ƃ��A �D���A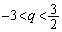
�����������q�́A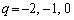
���̂����E�����̂́A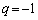
���̂Ƃ��A�A���A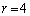
�C���A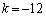
(iv) 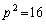 �C�܂�A
�C�܂�A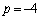 �̂Ƃ��A
�̂Ƃ��A �D���A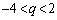
�����������q�́A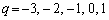
���̂����E�����̂́A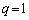
���̂Ƃ��A�A���A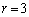
�C���A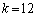
�ȏ���A
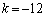 �̂Ƃ��A3����
�̂Ƃ��A3����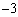 �C
�C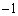 �C4�C
�C4�C
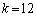 �̂Ƃ��A3����
�̂Ƃ��A3����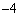 �C1�C3 ......[��]
�C1�C3 ......[��]
�ʉ��@�@�`�C�̂��ƁA�@�ŁA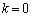 �Ƃ���ƁA
�Ƃ���ƁA
�ƂȂ��ӂ����Ȃ��̂ŁA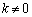 �ł���A
�ł���A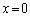 �͇@�̉��ɂ͂Ȃ�܂���B
�͇@�̉��ɂ͂Ȃ�܂���B
�@�ŁA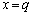 �C
�C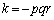 �Ƃ���ƁA
�Ƃ���ƁA
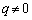 �Ȃ̂ŁA
�Ȃ̂ŁA
�A���Ap�Cr�͈ٕ����ŁA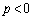 �C
�C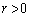 �ł����āA
�ł����āA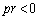
�]���āA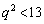 �ł���A
�ł���A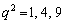 �Ɍ����܂��B
�Ɍ����܂��B
(i) 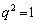 �̂Ƃ��A
�̂Ƃ��A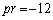
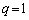 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A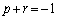 �C
�C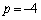 �C
�C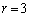 �C
�C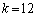
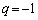 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A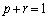 �C
�C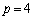 �C
�C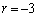 �C
�C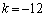
(ii) 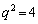 �̂Ƃ��A
�̂Ƃ��A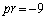
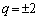 �Ȃ̂ŇA���A
�Ȃ̂ŇA���A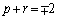 p�Cr�́A
p�Cr�́A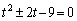 ��2���ŁA
��2���ŁA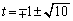 ���s�K�B
���s�K�B(iii) 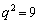 �̂Ƃ��A
�̂Ƃ��A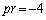
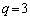 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A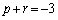 �C
�C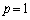 �C
�C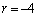 �C
�C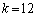
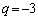 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A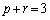 �C
�C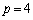 �C
�C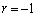 �C
�C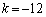 (i)�Ɠ������̑g���o�Ă��܂��B
(i)�Ɠ������̑g���o�Ă��܂��B
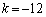 �̂Ƃ��A3����
�̂Ƃ��A3����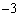 �C
�C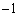 �C4�C
�C4�C
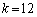 �̂Ƃ��A3����
�̂Ƃ��A3����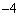 �C1�C3 ......[��]
�C1�C3 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B