�ꋴ�吔�w'06�N�O��[1]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̏���(a)�C(b)���Ƃ��ɂ݂������p�O�p�`���l����B�������A�Εӂ̒�����p�A���̑���2�ӂ̒�����q�Cr�Ƃ���B
(a) p�Cq�Cr�͎��R���ŁA���̂����̏��Ȃ��Ƃ�2�͑f���ł���B
(b) 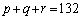
(1) q�Cr�̂ǂ��炩�͋����ł��邱�Ƃ������B
(2) p�Cq�Cr�̑g�����ׂċ��߂�B
���@�s�^�S���X�����ނƂ����������ł��B(1)���w���@�Ŏ����܂��B
�O�����̒藝���A
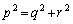 �@����@
�@����@
���������܂��B
(1) q�Cr���Ƃ��Ɋ���Ɖ��肵�܂��B
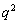 �C
�C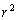 ����Ȃ̂ŁA
����Ȃ̂ŁA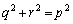 �͋����ł���Ap�������ł��Bp�������Ȃ�
�͋����ł���Ap�������ł��Bp�������Ȃ�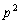 ��4�̔{���ł��Bc�Cd�����R���Ƃ��āA
��4�̔{���ł��Bc�Cd�����R���Ƃ��āA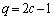 �C
�C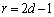
�Ƃ������Ƃ��ł��܂����A
�ł���A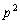 ��4�̔{���ɂȂ炸�A�������N���܂��B
��4�̔{���ɂȂ炸�A�������N���܂��B
�Ƃ������Ƃ́Aq�Cr���Ƃ��Ɋ���Ƃ�������͌��ł���Aq�Cr�̂ǂ��炩�͋����ł��B
(2) (1)���q�Cr�̂ǂ��炩�͋����Ȃ̂ŁAr���������Ƃ��āA
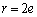 (e�͎��R��)�Ƃ����܂��B
(e�͎��R��)�Ƃ����܂��B
�@���A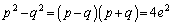 �@����A
�@����Ap�Cq�������ꂩ�������ő������������Ƃ���ƁA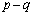 �C
�C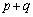 �͂Ƃ��Ɋ��
�͂Ƃ��Ɋ��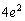 �ɓ������Ȃ邱�Ƃ͂���܂���B����āAp�Cq�͂Ƃ��Ɋ���Ƃ��ɋ�����(�Ƃ��ɋ������Ə���(a)�ɔ�����̂łƂ��Ɋ�ł�)�A
�ɓ������Ȃ邱�Ƃ͂���܂���B����āAp�Cq�͂Ƃ��Ɋ���Ƃ��ɋ�����(�Ƃ��ɋ������Ə���(a)�ɔ�����̂łƂ��Ɋ�ł�)�A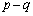 �C
�C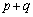 �͂Ƃ��ɋ����ł��Bk�Cm�����R�����Ƃ��āA
�͂Ƃ��ɋ����ł��Bk�Cm�����R�����Ƃ��āA �Ƃ����ƁA�A���A
�� 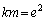
s�Ct�����R���Ƃ��āA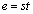 �Ƃ����ƁA
�Ƃ����ƁA �����ŁA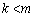 �Ȃ̂�
�Ȃ̂�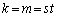 �Ƃ������Ƃ͂��蓾�܂���B����āA����(i)�C(ii)��2�̉\�����l�����܂��B
�Ƃ������Ƃ͂��蓾�܂���B����āA����(i)�C(ii)��2�̉\�����l�����܂��B (i) 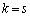 �C
�C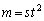 �̂Ƃ��A�B���A
�̂Ƃ��A�B���A 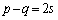 �C
�C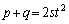
p�Cq�ɂ��ĉ����ƁA
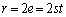 �Ȃ̂ŁA����(a)���A
�Ȃ̂ŁA����(a)���A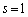 �Ɍ����܂��B����(b)���A
�Ɍ����܂��B����(b)���A�� 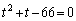
����āA���̏ꍇ�ɂ͏������݂���p�Cq�Cr�̑g�͂���܂���B
(ii) 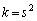 �C
�C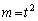 (
(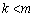 ���
���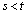 )�̂Ƃ��A�B���A
)�̂Ƃ��A�B���A ����(b)���A
�� 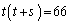
t��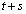 ��66�̖ł����A
��66�̖ł����A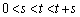 ���݂����̂́A
���݂����̂́A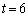 �C
�C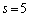 �݂̂ł��B
�݂̂ł��B
���̂Ƃ��A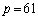 �C
�C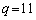 �C
�C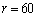
��L�ł́Ar�������Ƃ��čl���Ă��܂������Aq���������Ƃ��Ă��A�S�����l�ɂ��āA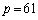 �C
�C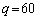 �C
�C
�������݂���p�Cq�Cr�̑g�́A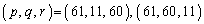 ......[��]
......[��]
�NjL�D��L�ł́A����(a)�����Ă���̂ŁA(i)�̏ꍇ���瓚���o�Ă��܂���ł������A����(a)���O���ƁA(i)��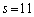 �C
�C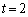 �Ƃ��āA
�Ƃ��āA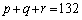 �ƂȂ�g
�ƂȂ�g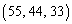 �������܂��B�悭�m��ꂽ3�ӂ̔䂪5�F4�F3�ƂȂ钼�p�O�p�`�ł��B
�������܂��B�悭�m��ꂽ3�ӂ̔䂪5�F4�F3�ƂȂ钼�p�O�p�`�ł��B
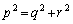 ���݂������R���̑g���s�^�S���X���ȂǂƌĂԂ��Ƃ�����܂��B�Ⴆ�A
���݂������R���̑g���s�^�S���X���ȂǂƌĂԂ��Ƃ�����܂��B�Ⴆ�A
�Ȃǂ��m���Ă��܂��B
��L��(i)�̏ꍇ�́A����(a)�����Ă���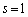 �Ɍ�����̂ł���A(ii)�̏ꍇ�Ɋ܂܂�܂��B(ii)�����Ă���ƁA���R��s�Ct�������Ă��āA
�Ɍ�����̂ł���A(ii)�̏ꍇ�Ɋ܂܂�܂��B(ii)�����Ă���ƁA���R��s�Ct�������Ă��āA
�Ƃ���ƁA�s�^�S���X���ƂȂ鎩�R���̑g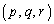 �������邱�Ƃ��킩��܂��B���ہA
�������邱�Ƃ��킩��܂��B���ہA
�ł��B
���啶�n'99���[5]�F
���R��a�Cb�Cc�ɂ��āA����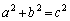 �����藧���A���Aa�Cb�݂͌��ɑf�Ƃ���B���̂Ƃ��A���̂��Ƃ��ؖ�����B
�����藧���A���Aa�Cb�݂͌��ɑf�Ƃ���B���̂Ƃ��A���̂��Ƃ��ؖ�����B (1) a����Ȃ�Ab�͋����ł���A����������c�͊�ł���B
(2) a����̂Ƃ��A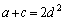 �ƂȂ鎩�R��d�����݂���B
�ƂȂ鎩�R��d�����݂���B
(1)�́A�{���(1)�Ɠ����ł��B
(2)�́A�{��(2)��(i)�̏ꍇ���A����(a)�������(ii)�̏ꍇ�Ɋ܂܂�āA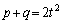 �ƕ\����A�Ƃ����Ƃ��납�猾���܂��B
�ƕ\����A�Ƃ����Ƃ��납�猾���܂��B
���嗝�n'92�O��[6]�ł́A�s�^�S���X����^����Q�������o�肳��Ă��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B