�ꋴ�吔�w'06�N�O��[3]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�傫�������ꂼ��5�C3�C1�̕��ʏ�̃x�N�g��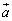 �C
�C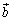 �C
�C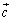 �ɑ��āA
�ɑ��āA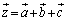 �Ƃ����B
�Ƃ����B
(1) 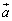 �C
�C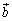 �C
�C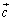 �����Ƃ��A
�����Ƃ��A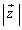 �̍ő�l�ƍŏ��l�����߂�B
�̍ő�l�ƍŏ��l�����߂�B (2) 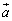 ���Œ肵�A
���Œ肵�A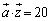 ���݂����悤��
���݂����悤��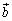 �C
�C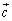 �����Ƃ��A
�����Ƃ��A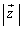 �̍ő�l�ƍŏ��l�����߂�B
�̍ő�l�ƍŏ��l�����߂�B
���@���W�n��ݒ肵����A�e�x�N�g���Ԃ̊p�̊����l�����肷��ƓD���Ƀn�}�荞�ނ��ƂɂȂ�܂��B�������Ɛ��U�@���������āA�����Ɋȕւɍl���邱�Ƃ��ł��邩�A�Ɠ���芷����Ƃ��낪�|�C���g�ł��傤�B
(1) 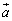 �C
�C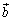 �̂Ȃ��p��α�C
�̂Ȃ��p��α�C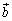 �C
�C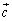 �̂Ȃ��p��β�C
�̂Ȃ��p��β�C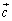 �C
�C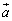 �̂Ȃ��p��γ�Ƃ���ƁA
�̂Ȃ��p��γ�Ƃ���ƁA �ł����A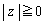 �Ȃ̂ŁA
�Ȃ̂ŁA 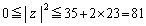 �@����@
�@����@�ƂȂ�܂��B���̕s�����̉E���̕s�����̓�������������̂́A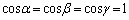 �C�܂�A
�C�܂�A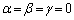 �ŁA3�̃x�N�g��
�ŁA3�̃x�N�g��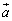 �C
�C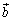 �C
�C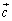 �����������������Ă���Ƃ��ł��B
�����������������Ă���Ƃ��ł��B
����āA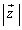 �̍ő�l�́A
�̍ő�l�́A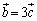 �C
�C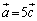 ��
��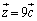 �ƂȂ�Ƃ��A
�ƂȂ�Ƃ��A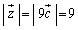 �ƂȂ�܂��B
�ƂȂ�܂��B
�@�̍����̕s�����̓�������������̂́A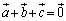 �̂Ƃ��ł����A�����Ȃ�\�������邩�ׂĂ݂܂��B
�̂Ƃ��ł����A�����Ȃ�\�������邩�ׂĂ݂܂��B
�܂��A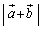 �ɂ��āA
�ɂ��āA 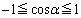 �Ȃ̂ŁA
�Ȃ̂ŁA�܂�A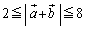 �@����A
�@����A
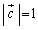 �Ȃ̂ŁA
�Ȃ̂ŁA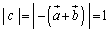 �C�܂�A
�C�܂�A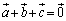 �Ƃ������Ƃ͂��蓾�܂���B�]���āA�@�̍����̕s�������������邱�Ƃ͂���܂���B�ł����A
�Ƃ������Ƃ͂��蓾�܂���B�]���āA�@�̍����̕s�������������邱�Ƃ͂���܂���B�ł����A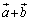 �ɂ��ćA������ꂽ�̂ŁA������g����
�ɂ��ćA������ꂽ�̂ŁA������g����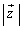 ���l���Ă݂܂��B
���l���Ă݂܂��B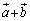 ��
��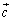 �̂Ȃ��p��θ �Ƃ��āA
�̂Ȃ��p��θ �Ƃ��āA 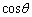 ���Œ肵�āA
���Œ肵�āA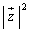 ��
��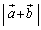 ��2�����Ƃ݂�ƁA
��2�����Ƃ݂�ƁA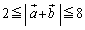 �C
�C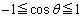 ���A
���A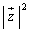 ��
��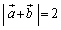 �̂Ƃ��ɍŏ��l���Ƃ�܂��B
�̂Ƃ��ɍŏ��l���Ƃ�܂��B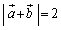 �̂Ƃ��A
�̂Ƃ��A�s�����̓����́A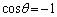 �̂Ƃ��ɐ������܂����A
�̂Ƃ��ɐ������܂����A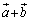 ��
��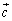 �����傤�Njt�����ɂȂ�Ƃ��ɁA
�����傤�Njt�����ɂȂ�Ƃ��ɁA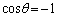 �ƂȂ�܂��B
�ƂȂ�܂��B
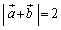 �́A�A�ɂ����č����̕s�����̓�������������Ƃ��ɋN����܂����A���̂Ƃ��A
�́A�A�ɂ����č����̕s�����̓�������������Ƃ��ɋN����܂����A���̂Ƃ��A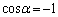 �C
�C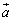 ��
��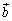 �͂��傤�Njt�����ŁA
�͂��傤�Njt�����ŁA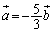 �ƂȂ��Ă��܂��B����ɁA
�ƂȂ��Ă��܂��B����ɁA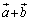 ��
��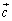 �����傤�Njt�����ŁA
�����傤�Njt�����ŁA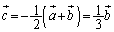 (
(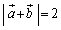 �C
�C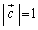 �ɒ���)�C�܂�A
�ɒ���)�C�܂�A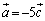 �C
�C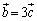 ��
��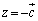 �̂Ƃ��A
�̂Ƃ��A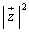 �͍ŏ��l1���Ƃ�A
�͍ŏ��l1���Ƃ�A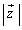 �͍ŏ��l1���Ƃ�܂��B
�͍ŏ��l1���Ƃ�܂��B
�ő�l�F9�C�ŏ��l�F1 ......[��]
(2) 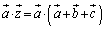
�� 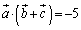 �@����B(1)�ł�
�@����B(1)�ł�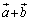 ���l���čŏ��l�����߂邱�Ƃ��ł����̂ŁA�����ł́A
���l���čŏ��l�����߂邱�Ƃ��ł����̂ŁA�����ł́A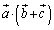 ���o�Ă���悤�ɂ��čl���邱�Ƃɂ��܂��B
���o�Ă���悤�ɂ��čl���邱�Ƃɂ��܂��B 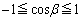 �Ȃ̂ŁA
�Ȃ̂ŁA

�܂�A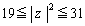 �@����C
�@����C
�C�̉E���̕s�����̓�������������̂́A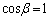 �C�܂�A
�C�܂�A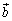 �C
�C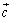 �����������ŁA
�����������ŁA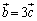 �ƂȂ�Ƃ��ɐ������܂��B
�ƂȂ�Ƃ��ɐ������܂��B
���̂Ƃ��A�B���A�� 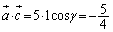 �C
�C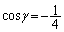
�ƂȂ�̂ŁA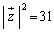 �ƂȂ�
�ƂȂ�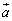 �C
�C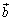 �C
�C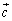 �̈ʒu�W�����蓾�܂��B����āA
�̈ʒu�W�����蓾�܂��B����āA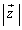 �̍ő�l��
�̍ő�l��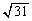 �ł��B
�ł��B
�C�̍����̕s�����̓�������������̂́A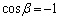 �C�܂�A
�C�܂�A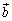 �C
�C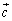 ���t�����ɂȂ�A
���t�����ɂȂ�A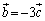 �ƂȂ�Ƃ��ɐ������܂��B
�ƂȂ�Ƃ��ɐ������܂��B
���̂Ƃ��A�B���A �� 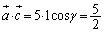 �C
�C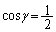
�ƂȂ�̂ŁA �ƂȂ�
�ƂȂ�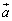 �C
�C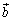 �C
�C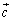 �̈ʒu�W�����蓾�܂��B����āA
�̈ʒu�W�����蓾�܂��B����āA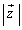 �̍ŏ��l��
�̍ŏ��l��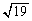 �ł��B
�ł��B
�ő�l�F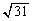 �C�ŏ��l�F
�C�ŏ��l�F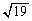 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B