�ꋴ�吔�w'07�N�O��[3]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
������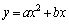 (
(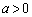 )��C�Ƃ���BC��ɈقȂ�2�_P�CQ���Ƃ�A����x���W�����ꂼ��p�Cq (
)��C�Ƃ���BC��ɈقȂ�2�_P�CQ���Ƃ�A����x���W�����ꂼ��p�Cq (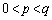 )�Ƃ���B
)�Ƃ���B
(1) ����OQ��C�ň͂܂ꂽ�����̖ʐς��A��OPQ�̖ʐς�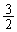 �{�ł���Ƃ��Ap��q�̊W�����߂�B�������AO�͌��_��\���B
�{�ł���Ƃ��Ap��q�̊W�����߂�B�������AO�͌��_��\���B (2) Q���Œ肵��P�����B��OPQ�̖ʐς��ő�ƂȂ�Ƃ���p��q�ŕ\���B�܂��A���̂Ƃ��́�OPQ�̖ʐςƁA����OQ��C�ň͂܂ꂽ�����̖ʐςƂ̔�����߂�B
���@��ϕ��̌����F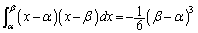 ���g������ł�(�e05�N�O��[4]�ł��o�肳��Ă��܂�)�B�����Ƃ��A���̖��ł́A
���g������ł�(�e05�N�O��[4]�ł��o�肳��Ă��܂�)�B�����Ƃ��A���̖��ł́A
�Ƃ��Ă��J�͂͂قƂ�Ǖς��Ȃ��A�Ƃ������A�������g����a��������̂�Y��邭�炢�Ȃ�f���Ɍv�Z���������ǂ����炢�ł����B
(1) ������C�F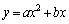 �@����@
�@����@ C��̓_P�CQ�̍��W�́A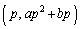 �C
�C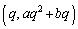 �ł��B
�ł��B
��OPQ�̖ʐ�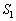 �́A
�́A ����OQ�́A�X��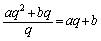 �Ō��_��ʂ钼���Ȃ̂ŁA
�Ō��_��ʂ钼���Ȃ̂ŁA 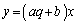 �@����A
�@����A�@�C�A�́A���_O�Ɠ_Q�Ō����A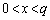 �ɂ����āA�A���@�̏�ɗ���̂ŁA����OQ��C�ň͂܂ꂽ�����̖ʐ�
�ɂ����āA�A���@�̏�ɗ���̂ŁA����OQ��C�ň͂܂ꂽ�����̖ʐ�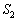 �́A
�́A 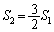 ���A
���A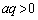 �Ŋ����Đ�������ƁA
�Ŋ����Đ�������ƁA�� 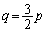 �܂���
�܂��� 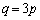 ......[��]
......[��]
(2) 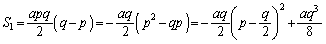
����́A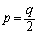 ......[��]�@�̂Ƃ��ɍő�ŁA
......[��]�@�̂Ƃ��ɍő�ŁA
���̂Ƃ��A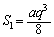
�NjL�D�����F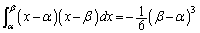 ���N�₩�Ɏg��������Љ�Ă����܂��B
���N�₩�Ɏg��������Љ�Ă����܂��B
�����C�m��'07�N[4]�F
(1) ���W���ʏ��2�̕�����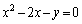 �C
�C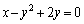 �̋��L�_���ׂĒʂ�~�̕����������߂�B
�̋��L�_���ׂĒʂ�~�̕����������߂�B (2) �A���s����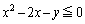 �C
�C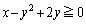 �̕\���̈�̖ʐς����߂�B
�̕\���̈�̖ʐς����߂�B
���@2�Ȑ�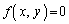 �C
�C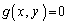 �����L�_P
�����L�_P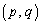 �����Ƃ���ƁAP�́A���Ȑ���̓_�Ȃ̂ŁA
�����Ƃ���ƁAP�́A���Ȑ���̓_�Ȃ̂ŁA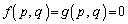 �ł��B
�ł��B
A�CB��萔�Ƃ��āA
�Ƃ��ē�����Ȑ��ɂ��āA
�ƂȂ�̂ŁAP�͋Ȑ�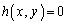 ��̓_�ł��B�@���(��)
��̓_�ł��B�@���(��)
(1) A�CB��萔�Ƃ��āA
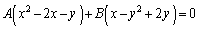 �@����@
�@����@�Ƃ����Ȑ��́A(��)���A2�������̋��L�_�����ׂĒʂ�܂��B�@������ƁA
�ƂȂ�܂����A���ꂪ�~��\�����߂ɁA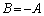 ���K�v�ł��B���̂Ƃ��A
���K�v�ł��B���̂Ƃ��A �@�����炩�̋Ȑ���\�����߂ɂ�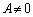 �C�����A�Ŋ���ƁA
�C�����A�Ŋ���ƁA 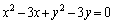 ......[��]
......[��]
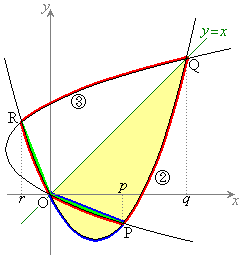 (2) �ʐς����߂�̈�́A�E�}�ŐԐ��Ɉ͂܂ꂽ�����ɂȂ�܂��B
(2) �ʐς����߂�̈�́A�E�}�ŐԐ��Ɉ͂܂ꂽ�����ɂȂ�܂��B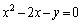 �@����A
�@����A
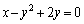 �@����B
�@����B�Ƃ��āA�A�C�B��A������ƁA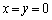 �Ƃ����������邱�Ƃ͂����ɂ킩��܂��B�A�C�B�̌�_��4����܂����A1�͌��_O�ł��B���̌�_���E�}�̂悤�ɁAP�CQ�CR�Ƃ��A���ꂼ���x���W��p�Cq�Cr�Ƃ��܂��B
�Ƃ����������邱�Ƃ͂����ɂ킩��܂��B�A�C�B�̌�_��4����܂����A1�͌��_O�ł��B���̌�_���E�}�̂悤�ɁAP�CQ�CR�Ƃ��A���ꂼ���x���W��p�Cq�Cr�Ƃ��܂��B
�������A�̎����E�̕����ƕ������B�̎���艺�̕����̌�_��P�C
�������A�̎����E�̕����ƕ������B�̎�����̕����̌�_��Q�C
�������A�̎���荶�̕����ƕ������B�̎�����̕����̌�_��R�C
�������A�̎���荶�̕����ƕ������B�̎���艺�̕����̌�_��O�ł��B
�A��x�Cy���t�ɂ���ƇB���ɂȂ�̂ŁA�A�ƇB�́A����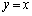 �Ɋւ��đΏ̂ł��B
�Ɋւ��đΏ̂ł��B
����āA���߂�ʐ�S�C�܂�E�}�ŐԐ��Ɉ͂܂ꂽ�����̖ʐς́A ����OQ�ƕ������B�̌�OP�ƕ������A�̌�PQ�ň͂܂ꂽ�����̖ʐ�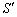 ��2�{��������
��2�{�������� �ɂȂ�܂��B
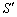 �́A����OQ�ƕ������A�̌�OQ�ň͂܂�镔��(�E�}�N���[���F����)�̖ʐ�
�́A����OQ�ƕ������A�̌�OQ�ň͂܂�镔��(�E�}�N���[���F����)�̖ʐ�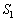 ����A�������B�̌�OP�ƕ������A�̌�OP�ň͂܂�镔���̖ʐ�
����A�������B�̌�OP�ƕ������A�̌�OP�ň͂܂�镔���̖ʐ�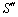 �����������̂ł��B
�����������̂ł��B
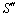 �́A����OP�ƕ������A�̌�OP�ň͂܂�镔��(�E�}�����͂ޕ���)�̖ʐ�
�́A����OP�ƕ������A�̌�OP�ň͂܂�镔��(�E�}�����͂ޕ���)�̖ʐ�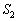 ����A����OP�ƕ������B�̌�OP�ň͂܂�镔��(�E�}���ΐF����)�̖ʐ�
����A����OP�ƕ������B�̌�OP�ň͂܂�镔��(�E�}���ΐF����)�̖ʐ�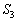 �����������̂ł��B
�����������̂ł��B
�A�ƇB������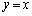 �Ɋւ��đΏ̂Ȃ��Ƃ���A
�Ɋւ��đΏ̂Ȃ��Ƃ���A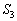 �́A����OR�ƕ������A�̌�OR�ň͂܂�镔���̖ʐςɓ������Ȃ�܂��B
�́A����OR�ƕ������A�̌�OR�ň͂܂�镔���̖ʐςɓ������Ȃ�܂��B
�A�F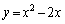 ��
��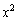 �̌W����1�Ȃ̂ŁA��ϕ��̌����F
�̌W����1�Ȃ̂ŁA��ϕ��̌����F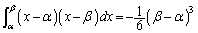 ��p����ƁA
��p����ƁA
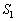 �̗̈�́A
�̗̈�́A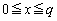 �ɂ���A
�ɂ���A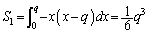
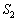 �̗̈�́A
�̗̈�́A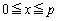 �ɂ���A
�ɂ���A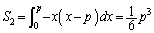
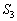 �̗̈�́A
�̗̈�́A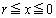 �ɂ���A
�ɂ���A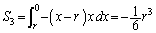
����āA �A�{�B���A
�� 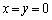 �܂���
�܂��� 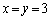 ����āA
����āA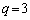 �ł��B
�ł��B
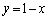 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A 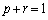 �C
�C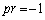
�C���A
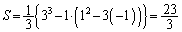 ......[��]
......[��]
�Ȃ��A���勳��'93�N�ɂ��A���l�̏o�肪����܂��B
xy���ʂɂ����āA�̈�A��A�F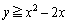 �ɂ���Ē�߂�B�̈�A��
�ɂ���Ē�߂�B�̈�A��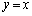 �Ɋւ��đΏ̂Ɉڂ����̈��B�Ƃ���Ƃ��A�̈�
�Ɋւ��đΏ̂Ɉڂ����̈��B�Ƃ���Ƃ��A�̈�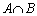 �̖ʐς����߂�B
�̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B