一橋大数学'08年前期[4]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
正四面体OABCの1辺の長さを1とする。辺OAを2：1に内分する点をP，辺OBを1：2に内分する点をQとし、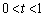
をみたすtに対して、辺OCをt：
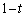に内分する点をRとする。
(1) PQの長さを求めよ。
(2) 
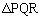の面積が最小となるときのtの値を求めよ。
解答 (1)はベクトルでも余弦定理でもOKですが、(2)の三角形の面積ではベクトルで行くべきでしょう。
，
，
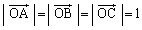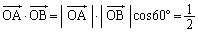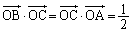(内積を参照)
，
，
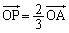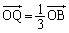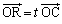
(1) 
∴ 
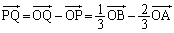
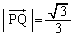......[答]
(2) 
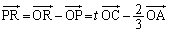
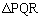の面積Sは、
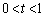において、S最小は、
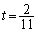......[答] のとき。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
