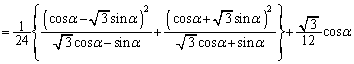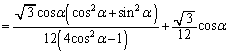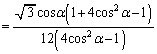慶大理工数学'06年[A3]
座標平面の原点Oを中心とする単位円周上に3点A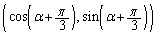
，B
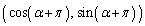，C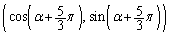
をとる(下図を参照)。ただし、
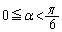とする。以下、(サ)〜(ス)は
，
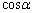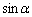を用いて、(セ)〜(タ)は
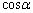を用いて記述しなさい。
線分ABとy軸との交点をD，線分BCとy軸との交点をEとすると、線分OD，線分OEの長さはそれぞれ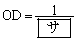
，
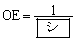である。
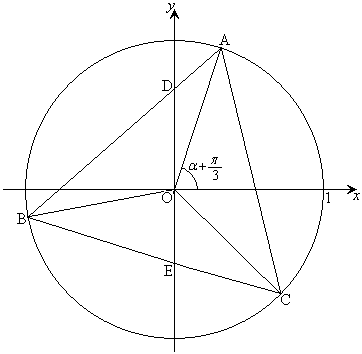このxy平面を含む座標空間において、正三角形ABC内の各点から、xy平面と垂直に、高さがその点のx座標の絶対値である線分を立てて得られる立体図形を考える。頂点A，B，Cの上にある線分の最上点をそれぞれF，G，Hとすると、三角錐OADFの体積は
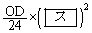，四角錐OACHFの体積は セ となる。
A，C，D，E，F，Hを頂点にもつ五面体の体積は、これら2つの錐体および三角錐OCEHの体積の和であり、 ソ となる。また、三角錐BDEGの体積は タ となる。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
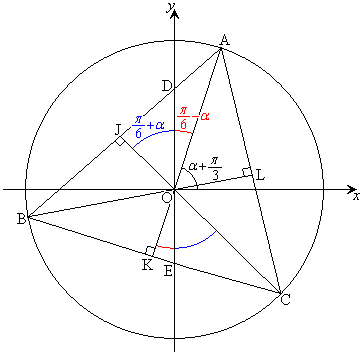解答 立体図形の問題ですが、誘導通りに進めれば手強くありません。なお、三角比、三角形の面積を参照してください。
(サ) 原点Oから辺AB，BC，CAに下ろした垂線の足をJ，K，Lとします。
(
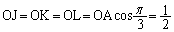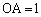)右図より、
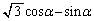......[答]
(シ)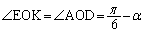 
より、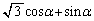 
......[答]
(ス) 三角錐OADFを、底面：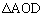
，高さ：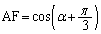
(＝点Aのx座標の絶対値)の三角錐と見ると、 三角錐OADFの体積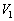
は、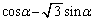 
......[答]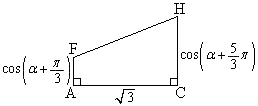
(セ) 四角錐OACHFを、右図の台形ACHFが底辺、高さ：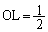
の四角錐と見ると、台形ACHFの面積は、
，
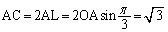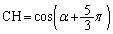(＝点Cのx座標の絶対値)より、 四角錐OACHFの体積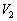
は、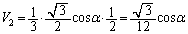 
......[答]
(ソ) 三角錐OECHを、底面：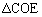
，高さ：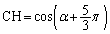
の三角錐と見ると、
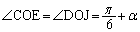より、 三角錐OECHの体積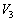
は、
A，C，D，E，F，Hを頂点にもつ五面体の体積Vは、
(タ) 三角錐BDEGを、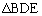
を底面とし、高さ：
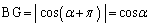(＝点Bのx座標の絶対値)の三角錐と見ると、 三角錐BDEGの体積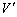
は、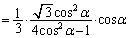 
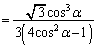......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
......[答]
