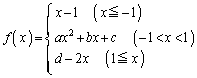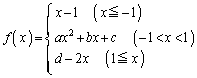慶應大学理工学部2006年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[A1](1) a，b，c，dは実数とする。関数
がすべてのxで微分可能であるとき、a＝ ア ，d＝ イ である。
(2) 定積分
の値は ウ となる。
(3) α，βは実数とする。どのような実数p，qに対しても
となるのは、α＝ エ ，β＝ オ のときである。
[解答へ]
[A2] ある時点(0年目)で、同じ容量の2つの空の樽A，Bに新味噌を一杯に入れ、以後、1年経つごとに以下の操作を行う。ただし味噌の量は自然には増減しないとする。
Bの味噌を半分取り除き、Aの味噌の半分をBに移す。さらに、Aにはその年の新味噌を入れ一杯にし、両樽ともよく混ぜる。
以下では、新味噌は0年物とし、x年物の味噌が1年経過したものを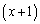
年物とする。また、x年物とy年物を同量ずつ混ぜた味噌は
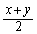年物と呼ぶ。
n年後に上記の操作を行った直後のA，Bの味噌をそれぞれ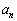
年物、
年物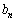と表す。例えば
，
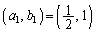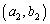＝ カ となる。
自然数nに対し、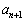
を
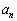で表すと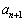
＝ キ となり、数列
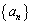の一般項は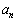
＝ ク となる。この式を用いることで、数列
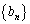の漸化式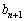
＝ ケ を得る。ここで
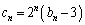とおき、数列
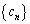の一般項を求めることにより、数列
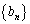の一般項は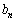
＝ コ となることがわかる。
[解答へ]
[A3] 座標平面の原点Oを中心とする単位円周上に3点A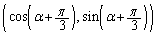
，B
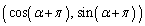，C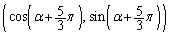
をとる(下図を参照)。ただし、
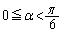とする。以下、(サ)〜(ス)は
，
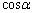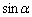を用いて、(セ)〜(タ)は
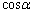を用いて記述しなさい。
線分ABとy軸との交点をD，線分BCとy軸との交点をEとすると、線分OD，線分OEの長さはそれぞれ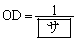
，
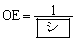である。
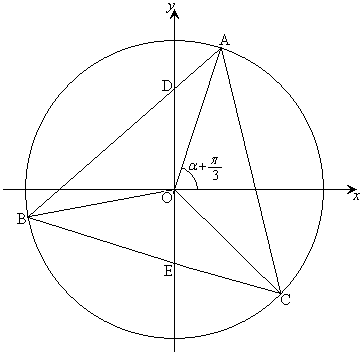このxy平面を含む座標空間において、正三角形ABC内の各点から、xy平面と垂直に、高さがその点のx座標の絶対値である線分を立てて得られる立体図形を考える。頂点A，B，Cの上にある線分の最上点をそれぞれF，G，Hとすると、三角錐OADFの体積は
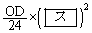，四角錐OACHFの体積は セ となる。
A，C，D，E，F，Hを頂点にもつ五面体の体積は、これら2つの錐体および三角錐OCEHの体積の和であり、 ソ となる。また、三角錐BDEGの体積は タ となる。
[解答へ]
[A4](1) 積分
(
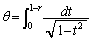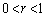)において、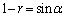
(
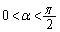)とおくと、
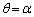であることを示しなさい。 (2) 関数
(
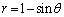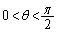)を極方程式とする座標平面上(x，y座標)の曲線を考える。偏角θ をもつ点における接線の傾き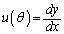
は、θ を用いて表すと
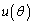＝ チ となり、 
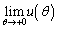＝ ツ ，
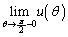＝ テ である。
(3) (2)の曲線において、y座標が最大となる点を求め、曲線の概形を図示しなさい。解答は計算も含めて解答欄に書きなさい。
[解答へ]
[B1] 整数p，q，r，α，β に対し、次のようなx，yについての連立1次方程式を考える。
以下では、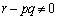
とする。
(1) 解x，yをp，q，r，α，β を用いて表しなさい。解答欄には答だけを書きなさい。
(2) 整数p，q，rに関する条件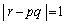
は、任意の整数α，β に対し解x，yが整数であるための必要十分条件であることを証明しなさい。 (3) 
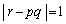のとき、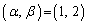
に対する解のxの値が2となるような整数の組
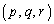をすべて求めなさい。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
