慶大理工数学'06年[A4]
(1) 積分
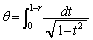 (
(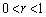 )
)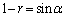 (
(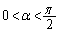 )とおくと、
)とおくと、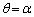 であることを示しなさい。
であることを示しなさい。
(2) 関数
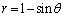 (
(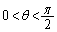 )
)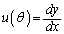 は、θ を用いて表すと
は、θ を用いて表すと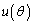 = チ となり、
= チ となり、
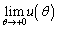 = ツ ,
= ツ ,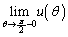 = テ
= テ
(3) (2)の曲線において、y座標が最大となる点を求め、曲線の概形を図示しなさい。解答は計算も含めて解答欄に書きなさい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (1) 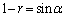 (
(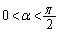 )とおくと、
)とおくと、
(2)(チ) 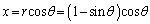
∴ 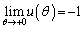 ......[答]
......[答] (テ) 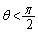 として
として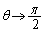 とすると、
とすると、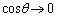 ,
,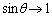 より、
より、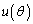 は分母も分子もともに0に近づきます。
は分母も分子もともに0に近づきます。 分子で0に近づくのは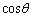 ,分母で0に近づくのは
,分母で0に近づくのは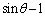
これを分母、分子で約分できる形とするために、分母・分子に、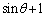 をかけます(不定形の極限を参照)。
をかけます(不定形の極限を参照)。 ∴ 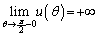 ......[答]
......[答] 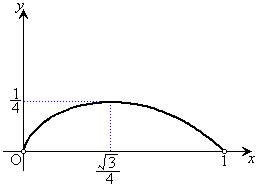
(3) 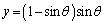
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。