�c�嗝�H���w'06�N[B1]
����p�Cq�Cr�Cα�Cβ �ɑ��A���̂悤��x�Cy�ɂ��Ă̘A��1�����������l����B
�ȉ��ł́A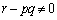 �Ƃ���B
�Ƃ���B
(1) ��x�Cy��p�Cq�Cr�Cα�Cβ ��p���ĕ\���Ȃ����B���ɂ͓������������Ȃ����B
(2) ����p�Cq�Cr�Ɋւ������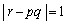 �́A�C�ӂ̐���α�Cβ �ɑ���x�Cy�������ł��邽�߂̕K�v�\�������ł��邱�Ƃ��ؖ����Ȃ����B
�́A�C�ӂ̐���α�Cβ �ɑ���x�Cy�������ł��邽�߂̕K�v�\�������ł��邱�Ƃ��ؖ����Ȃ����B (3) 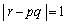 �̂Ƃ��A
�̂Ƃ��A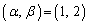 �ɑ������x�̒l��2�ƂȂ�悤�Ȑ����̑g
�ɑ������x�̒l��2�ƂȂ�悤�Ȑ����̑g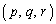 �����ׂċ��߂Ȃ����B
�����ׂċ��߂Ȃ����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������s���̗Z�����ł��B
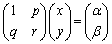 �@����@
�@����@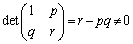 ���A
���A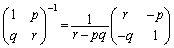 �����݂���(�t�s�����Q��)�A�@�̗��ӂɍ����炩����(�s��̐����Q��)�ƁA
�����݂���(�t�s�����Q��)�A�@�̗��ӂɍ����炩����(�s��̐����Q��)�ƁA
(2) (1)�̌��ʂ��A����p�Cq�Cr��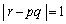 �C�܂�A
�C�܂�A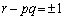 �����Ƃ��A�C�ӂ̐���α�Cβ �ɑ��A��x�Cy�C�����A
�����Ƃ��A�C�ӂ̐���α�Cβ �ɑ��A��x�Cy�C�����A 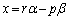 �C
�C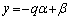
�܂��́A
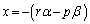 �C
�C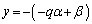
�͂�����������ɂȂ�܂��B
�t�ɁA�C�ӂ̐���α�Cβ �ɑ���x�Cy�������ł���Ƃ��A(1)�̌��ʂ��A
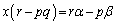 �@����A
�@����A
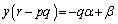 �@����B
�@����B�A���Ap�Cr�̍ő����d�C�܂��A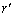 �C
�C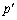 �𐮐��Ƃ��āA
�𐮐��Ƃ��āA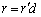 �C
�C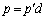 �Ƃ�����(���̂Ƃ��A
�Ƃ�����(���̂Ƃ��A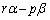 ��d�̔{��)�A
��d�̔{��)�A 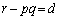 �ł���A
�ł���A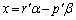 �͐����ɂȂ�܂����A
�͐����ɂȂ�܂����A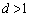 (�܂���
(�܂���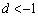 )�ł����Ă��悢���ƂɂȂ�܂��B
)�ł����Ă��悢���ƂɂȂ�܂��B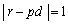 �ł���K�v�͂���܂���B
�ł���K�v�͂���܂���B
�������A�B�ł́Aα�Cβ ���C�ӂ̐������Ƃ�Ƃ��A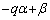 �͔C�ӂ̐������Ƃ蓾�܂��B
�͔C�ӂ̐������Ƃ蓾�܂��B
�C�ӂ̐������Ƃ肤��Ƃ������Ƃ́A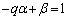 �ƂȂ邱�Ƃ����蓾��Ƃ������Ƃł�(�Ⴆ�A
�ƂȂ邱�Ƃ����蓾��Ƃ������Ƃł�(�Ⴆ�A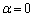 �C
�C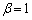 �̂Ƃ�)�B
�̂Ƃ�)�B
���̂Ƃ��A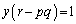 ����y�������ƂȂ邽�߂ɂ́A
����y�������ƂȂ邽�߂ɂ́A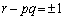
���̂Ƃ��A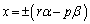 �������ł��B
�������ł��B
�]���āA�C�ӂ̐���α�Cβ �ɑ���x�Cy�������ł���Ƃ��A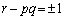
�ȏ���A����p�Cq�Cr�Ɋւ������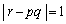 �́A�C�ӂ̐���α�Cβ �ɑ���x�Cy�������ł��邽�߂��K�v�\�������ł��B
�́A�C�ӂ̐���α�Cβ �ɑ���x�Cy�������ł��邽�߂��K�v�\�������ł��B
(3) 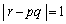 �̂Ƃ��A
�̂Ƃ��A 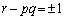 �C
�C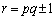
�E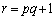 �̂Ƃ��A
�̂Ƃ��A �D�|�C�~q���A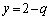
�C���A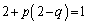
�� 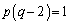
p�Cq�͐���������A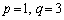 �܂���
�܂��� 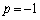 �C
�C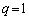
�O�҂̂Ƃ��A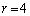 �C
�C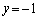 �C��҂̂Ƃ��A
�C��҂̂Ƃ��A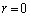 �C
�C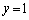
�E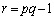 �̂Ƃ��A
�̂Ƃ��A �C�~q�|�D���A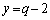
�C���A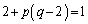
�� 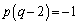
p�Cq�͐���������A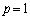 �C
�C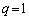 �܂���
�܂��� 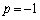 �C
�C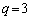
�O�҂̂Ƃ��A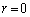 �C
�C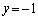 �C��҂̂Ƃ��A
�C��҂̂Ƃ��A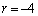 �C
�C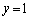
�� 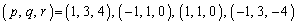 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B