(1) a�Cb�Cc�Cd�͎����Ƃ���B��
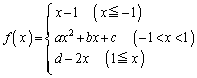
�����ׂĂ�x�Ŕ����\�ł���Ƃ��Aa���@�A�@�Cd���@�C�@�ł���B
(2) ��ϕ�
�̒l���@�E�@�ƂȂ�B
(3) α�Cβ�͎����Ƃ���B�ǂ̂悤�Ȏ���p�Cq�ɑ��Ă�
�ƂȂ�̂́Aα���@�G�@�Cβ���@�I�@�̂Ƃ��ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�y�L���z�L���͂����܂łł��B
�]���āA�S�Ă�x��
���ӂ́A
�E�ӂ́A
���A
�� 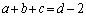 �@����B
�@����B
�܂��A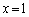 �ɂ����č��������W���ƉE�������W������v���邱�Ƃ��K�v�ŁA
�ɂ����č��������W���ƉE�������W������v���邱�Ƃ��K�v�ŁA
�܂��A
���ӂ́A
�E�ӂ́A
�� 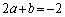 �@����C
�@����C
�C�|�A���A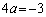
��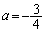 ......[��]
......[��]
�C�|�A���A
��
(�C) �C���A
�@���A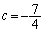
�B���A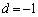 ......[��]
......[��]
�B���A
(2)(�E) 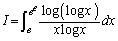
(3)(�G)(�I) 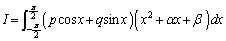
��
���ꂪ�A�ǂ̂悤�Ȏ���p�Cq�ɂ��Ă����藧���߂ɂ́A
�� 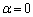 �C
�C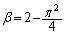 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��w�y�w�m ���������t���I
���n��w�l�b�g�m��w�y�w�m
(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B
���n��w�l�b�g�m��w�y�w�m
(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B