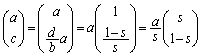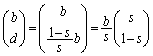���嗝�n���w'01�N���[5]
�s��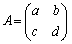 ����ю���x�ɑ��A�s���p���ĕ\���ꂽx�Cy�Ɋւ���2�̘A��1��������
����ю���x�ɑ��A�s���p���ĕ\���ꂽx�Cy�Ɋւ���2�̘A��1��������
(i) 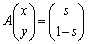 �C(ii)
�C(ii) 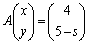
�ɂ��āA���̏���(��)���l����B
(��) ������(i)�ɂ͉������݂��āA������(ii)�ɂ͉������݂��Ȃ��B
���̂Ƃ��A���̖₢�ɓ�����B
(1) ����(��)�����藧�Ƃ��A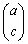 �C
�C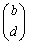 �́A�������
�́A�������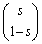 �̎����{�ł��邱�Ƃ������B
�̎����{�ł��邱�Ƃ������B (2) ����(��)���݂���2�̘A������������邱�Ƃ��ł��邽�߂�s�̏��������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@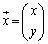 ��x�Cy�𖢒m���C
��x�Cy�𖢒m���C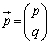 ��p�Cq��^����ꂽ�萔�Ƃ��āA2���������s��
��p�Cq��^����ꂽ�萔�Ƃ��āA2���������s�� ��p���ĕ\������A���������F
��p���ĕ\������A���������F
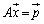 �@����@
�@����@
���l���܂��B
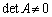 �ł����
�ł����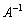 �����݂���̂ŁA�@���ӂ̍�����
�����݂���̂ŁA�@���ӂ̍�����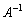 �������āA
�������āA
���ꂪ�A���������@�̉���^���܂��B�����A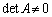 �ł���ΘA���������@�͉��������܂��B
�ł���ΘA���������@�͉��������܂��B
 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A
�E�A�̕\�������ƇB�̕\������������̒����ł��邩�A�܂��́A�ǂ��炩����݂̂�������\���ꍇ�A�����A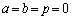 �C�܂��́A
�C�܂��́A �C
�C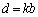 �C
�C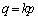 �ƂȂ����k�����݂���ꍇ�ɂ́Aa�Cb�̂����ꂩ�����0�łȂ���Β���
�ƂȂ����k�����݂���ꍇ�ɂ́Aa�Cb�̂����ꂩ�����0�łȂ���Β��� ��̂��ׂĂ̓_�A�܂��́A
��̂��ׂĂ̓_�A�܂��́A �ł���Β���
�ł���Β��� ��̂��ׂĂ̓_�̍��W
��̂��ׂĂ̓_�̍��W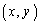 ���A���������̉��ɂȂ�܂����A������ɂ��Ă����������ɂ�����1�Ɍ��܂�Ȃ��̂ŁA�u�s��v�ƌ����܂��B
���A���������̉��ɂȂ�܂����A������ɂ��Ă����������ɂ�����1�Ɍ��܂�Ȃ��̂ŁA�u�s��v�ƌ����܂��B �E�A�̕\�������ƇB�̕\�����������s�ňقȂ钼���ł���ꍇ�A�A���������͉��������܂���B���̏ꍇ���A�u�s�\�v�ƌ����܂��B
�{��́A������(ii)�ɉ����Ȃ��A�s�\�ł���A�ƌ����Ă���̂ŁA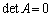 �ł����A������(i)�ɂ͉������݂���̂ŁA������(i)�͕s��ł��邱�ƂɂȂ�܂��B
�ł����A������(i)�ɂ͉������݂���̂ŁA������(i)�͕s��ł��邱�ƂɂȂ�܂��B
(1) ������(ii)�ɉ������݂��Ȃ��̂� �͑��݂����A
�͑��݂����A 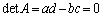 �@����C
�@����C�C�ɂ�������炸�A�A��������(i)�F
���������̂ŁA�D�ƇE�͓���̒�����\���������ɂȂ邩�A�܂��́A�ǂ��炩����݂̂�������\���܂��B(i) �D��������\���Ȃ��Ƃ��A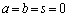
(ii) �E��������\���Ȃ��Ƃ��A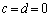 �C
�C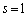
(iii) �D�ƇE������̒�����\���Ƃ��A
�E �̂Ƃ��A�C���
�̂Ƃ��A�C���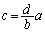 �ł����A�D�ƇE������̒�����\�����߂ɁA
�ł����A�D�ƇE������̒�����\�����߂ɁA ������ �Ƃ����
�Ƃ����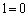 �ɂȂ��Ă��܂��̂�
�ɂȂ��Ă��܂��̂�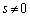 ���A
���A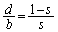 �C����āA
�C����āA �E �̂Ƃ��A�D�ƇE������̒�����\�����߂ɁA
�̂Ƃ��A�D�ƇE������̒�����\�����߂ɁA
�܂��A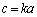 �C
�C ��������k�����݂��܂��B����āA
��������k�����݂��܂��B����āA �ȏ���A �C
�C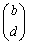 �́A�������
�́A�������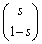 �̎����{�ł��B
�̎����{�ł��B
(2) (1)���Ak�Ch�������Ƃ��āA
�Ƃ����܂��B �̂Ƃ��ɂ́A�A������������邱�Ƃ��ł��Ȃ��̂ŁAk�Ch�̂ǂ��炩�����0�ł͂���܂���B
�̂Ƃ��ɂ́A�A������������邱�Ƃ��ł��Ȃ��̂ŁAk�Ch�̂ǂ��炩�����0�ł͂���܂���B
�A��������(i)�́A ���̂Ƃ��A(i)�́A (�F��������\���Ȃ�)�C
(�F��������\���Ȃ�)�C (�G��������\���Ȃ�)�̏ꍇ���܂߂āA
(�G��������\���Ȃ�)�̏ꍇ���܂߂āA ����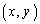 �����ɂ����܂��B
�����ɂ����܂��B
�A��������(ii)�́A ���ꂪ���������Ȃ��Ƃ������Ƃ́A�H�̂���킷�����ƇI�̕\�����������s�ňقȂ钼�����Ƃ������Ƃł��B�H���A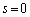 �Ƃ������Ƃ͂��肦�܂���B�H��
�Ƃ������Ƃ͂��肦�܂���B�H�� �����������ƇI���قȂ钼����\�����߂̏����́A
�����������ƇI���قȂ钼����\�����߂̏����́A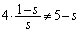
����āA����(��)���݂���2�̘A������������邱�Ƃ��ł��邽�߂�s�̏����́A ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B