���嗝�n���w'02�N�O��[2]
���a1�̉~����ɑ��قȂ�3�_A�CB�CC������B
(1) 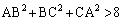 �Ȃ��
�Ȃ��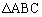 �͉s�p�O�p�`�ł��邱�Ƃ������B
�͉s�p�O�p�`�ł��邱�Ƃ������B (2)  ���������邱�Ƃ������B�܂��A���̓�������������̂͂ǂ̂悤�ȏꍇ���B
���������邱�Ƃ������B�܂��A���̓�������������̂͂ǂ̂悤�ȏꍇ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�D�ꂽ��@������悤�ł����A�v�������l�͂���ŗǂ��ł����A������ł͉��L�̂悤�Ȃ��̂ł��傤�B���ł��B
�@���ӂ� ��������ƁA
��������ƁA �� 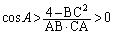 (�� BC�͉~�̒��a2����������)���l�ɁA
(�� BC�͉~�̒��a2����������)���l�ɁA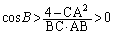 �C
�C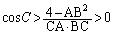
����āAA�CB�CC���ׂĉs�p������A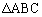 �͉s�p�O�p�`�B
�͉s�p�O�p�`�B
(2) �~�̒��S��O�C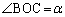 �C
�C �C
�C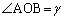 �Ƃ��܂��B
�Ƃ��܂��B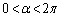 �C
�C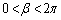 �C
�C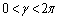 �C
�C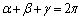 �C
�C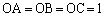 �ł��B
�ł��B (α�Cβ�Cγ�́A�O�p�`�̓��p�ł͂Ȃ��A�O�p�`�̊O�S�Ɗe���_�����Ԑ������m�̂Ȃ��p�ł��邱�ƁA�܂��A�O�p�`���݊p�O�p�`�̏ꍇ�Aα�Cβ�Cγ�̂ǂꂩ���݊p�ɑ��钆�S�p�ɂȂ�Ƃ��ɂ́A �����傫�Ȋp�ɂȂ邱�Ƃɒ���)�]���藝���A
�����傫�Ȋp�ɂȂ邱�Ƃɒ���)�]���藝���A  ����A
����A
�Ƃ����܂��B�����ŁA
 �@����B
�@����B�ł��B
(i) 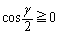 �C�܂�A
�C�܂�A �̂Ƃ��A�B�̊e�ӂ�
�̂Ƃ��A�B�̊e�ӂ� (
( )��������
)��������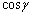 �������邱�Ƃɂ��A
�������邱�Ƃɂ��A 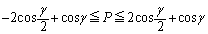 ����C
����C�����̓����́A �C�܂�A
�C�܂�A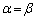 �̂Ƃ��ɐ����B
�̂Ƃ��ɐ����B
�E���̓����́A �C�܂�A
�C�܂�A �̂Ƃ��ɐ����B
�̂Ƃ��ɐ����B (ii) 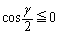 �C�܂�A
�C�܂�A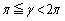 �̂Ƃ��A�B�̊e�ӂ�
�̂Ƃ��A�B�̊e�ӂ�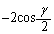 (
(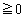 )��������
)��������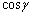 �������邱�Ƃɂ��A
�������邱�Ƃɂ��A  ����D
����D�����̓����́A �C�܂�A
�C�܂�A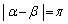 �̂Ƃ��ɐ����B
�̂Ƃ��ɐ����B
�E���̓����́A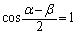 �C�܂�A
�C�܂�A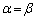 �̂Ƃ��ɐ����B
�̂Ƃ��ɐ����B �����ŁA �Ƃ����āA
�Ƃ����āA
(i)�̂Ƃ��A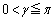 ���A
���A
���̂Ƃ��A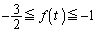 �C
�C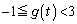
�C���A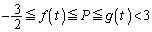
�����ŁA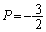 �ƂȂ�̂́A
�ƂȂ�̂́A ���A
���A �C�܂�A
�C�܂�A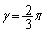 �̂Ƃ��A
�̂Ƃ��A
�����A �̂Ƃ��ŁA���̂Ƃ��A
�̂Ƃ��ŁA���̂Ƃ��A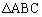 �͐��O�p�`�ł��B
�͐��O�p�`�ł��B
(ii)�̂Ƃ��A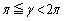 ���A
���A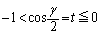
���̂Ƃ��A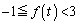 �C
�C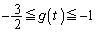
�D���A
�����ŁA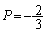 �ƂȂ�̂́A
�ƂȂ�̂́A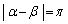 ���A
���A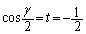 �C�܂�A
�C�܂�A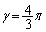 �̂Ƃ��ł����A���̂Ƃ��A
�̂Ƃ��ł����A���̂Ƃ��A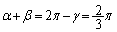 �ŁA
�ŁA �C
�C �Ȃ̂ŁA
�Ȃ̂ŁA �ɂ͂Ȃ蓾�܂���B
�ɂ͂Ȃ蓾�܂���B �ȏ���A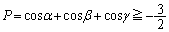 �ł����āA���������́A
�ł����āA���������́A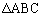 �����O�p�`�̂Ƃ��ł��B
�����O�p�`�̂Ƃ��ł��B
�A���A �ł����āA���������́A
�ł����āA���������́A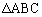 �����O�p�`�̂Ƃ� ......[��]
�����O�p�`�̂Ƃ� ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B