���嗝�n���w'04�N�O��[5]
���f��α�ɑ��Ă��̋��f����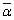 �ł���킷�Bα�������ł͂Ȃ����f���Ƃ���B���f���ʓ��̉~C���A1�C
�ł���킷�Bα�������ł͂Ȃ����f���Ƃ���B���f���ʓ��̉~C���A1�C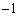 �Cα��ʂ�Ȃ�AC��
�Cα��ʂ�Ȃ�AC��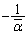 ���ʂ邱�Ƃ������B(���ӁF���f���ʂ̂��Ƃf�����ʂƂ�����)
���ʂ邱�Ƃ������B(���ӁF���f���ʂ̂��Ƃf�����ʂƂ�����)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���s�ے��ɂ����Ă͔͈͊O�̖��ł����A�v�Z�����́A���s�ے��őΉ��ł��܂��B
�~C�̒��S��\�����f����c�Ƃ���B1�C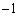 �Cα���~C��̓_�ł��邱�Ƃ��A
�Cα���~C��̓_�ł��邱�Ƃ��A
�e��2�悷���(��Βl�Q��)�A
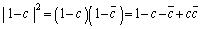 ����@
����@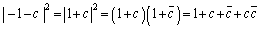
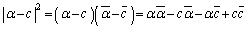
����āA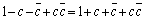 ����A
����A
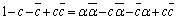 ����B
����B
�A���A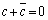 ����C
����C
�B�C�C���A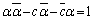 ����D
����D
�@�C�C���A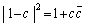 ����E
����E
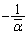 ��c�Ƃ̋�����2��ɂ��āA
��c�Ƃ̋�����2��ɂ��āA
(�D��p����ƁA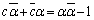 )
)
����āA�E���A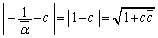
������A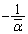 �Ɖ~C�̒��Sc�Ƃ̋����͉~C�̔��a�ɓ������A
�Ɖ~C�̒��Sc�Ƃ̋����͉~C�̔��a�ɓ������A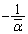 �͉~C��̓_�ł��B
�͉~C��̓_�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B