京都大学理系2004年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1]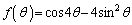 
とする。
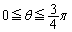における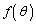
の最大値および最小値を求めよ。
[解答へ]
[2]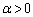 
とし、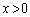
で定義された関数
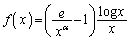を考える。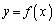
のグラフより下側でx軸より上側の部分の面積をαで表せ。ただし、eは自然対数の底である。
[解答へ]
[3] nを2以上の自然数とする。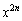
を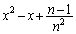
で割った余りを
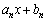とする。すなわち、xの多項式
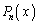があって
が成り立っているとする。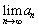
，
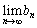を求めよ。
[解答へ]
[4] 行列A，Bを
，
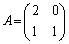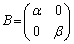
(＊) どんな2次正方行列Yに対しても、2次正方行列Xで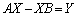
となるものがある。 [解答へ]
[5] 複素数αに対してその共役複素数を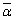
であらわす。αを実数ではない複素数とする。複素平面内の円Cが、1，
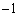，αを通るならば、Cは
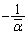も通ることを示せ。(注意：複素平面のことを複素数平面ともいう)
[解答へ]
[6] Nを自然数とする。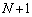
個の箱があり、1から
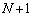までの番号が付いている。どの箱にも玉が1個入っている。番号1からNまでの箱に入っている玉は白玉で、番号
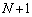の箱に入っている玉は赤玉である。次の操作(＊)を、おのおのの
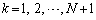に対して、kが小さい方から順番に1回ずつ行う。
(＊) k以外の番号のN個の箱から1個の箱を選び、その箱の中身と番号kの箱の中身を交換する。(ただし、N個の箱から1個の箱を選ぶ事象は、どれも同様に確からしいとする。)
操作がすべて終了した後、赤玉が番号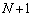
の箱に入っている確率を求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 