京大理系数学'05年前期[3]
α，β，γは相異なる複素数で、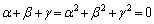
を満たすとする。このとき、α，β，γの表す複素平面上の3点を結んで得られる三角形はどのような三角形か。(ただし、複素平面を複素数平面ともいう。)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 この問題は、現行課程では範囲外の問題です。なお、複素数平面を参照してください。
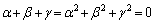より、
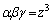とおくと、3次方程式の解と係数の関係より、α，β，γは、3次方程式：
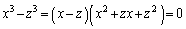の3解であって、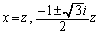
相異なる複素数α，β，γは、z，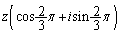
，
(
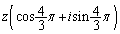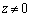です)のいずれか3個であって、これら3複素数で正三角形を作ります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2023(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
