京大理系数学'06年前期[4]
2以上の自然数nに対し、nと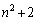 がともに素数になるのは
がともに素数になるのは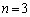 の場合に限ることを示せ。
の場合に限ることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 nが素数となるものを、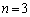 を除いて書き並べてみます。
を除いて書き並べてみます。
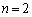 のとき、
のとき、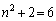 ,
,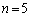 のとき、
のとき、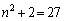 ,
,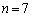 のとき、
のとき、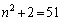 ,
,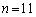 のとき、
のとき、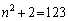 ,
,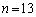 のとき、
のとき、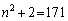
こう書いてみると、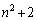 がいずれも3の倍数であることに気付きます。
がいずれも3の倍数であることに気付きます。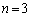 を除いて、
を除いて、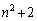 が3の倍数になることを言えば、題意が言えることになります。
が3の倍数になることを言えば、題意が言えることになります。
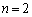 のとき、
のとき、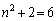 は3の倍数であって、素数ではありません。
は3の倍数であって、素数ではありません。
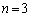 のとき、
のとき、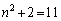 は素数です。
は素数です。
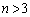 となる素数nについて、nは3の倍数ではないので、kを整数として、
となる素数nについて、nは3の倍数ではないので、kを整数として、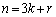 とおくと、
とおくと、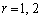 に限られます。
に限られます。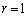 のとき、
のとき、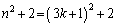
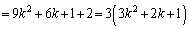 は、3の倍数であって素数ではありません。
は、3の倍数であって素数ではありません。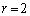 のとき、
のとき、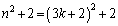
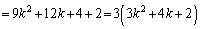 は、3の倍数であって素数ではありません。
は、3の倍数であって素数ではありません。
以上より、nと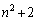 がともに素数となるのは
がともに素数となるのは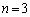 の場合に限られます。
の場合に限られます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。