京大理系数学'08年乙[6]
地球上の北緯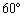 東経
東経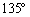 の地点をA,北緯
の地点をA,北緯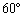 東経
東経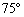 の地点をBとする。AからBに向かう2種類の飛行経路
の地点をBとする。AからBに向かう2種類の飛行経路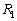 ,
,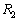 を考える。
を考える。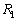 は西に向かって同一緯度で飛ぶ経路とする。
は西に向かって同一緯度で飛ぶ経路とする。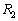 は地球の大円に沿った経路のうち飛行距離の短い方とする。
は地球の大円に沿った経路のうち飛行距離の短い方とする。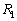 に比べて
に比べて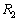 は飛行距離が3%以上短くなることを示せ。ただし地球は完全な球体であるとし、飛行機は高度0を飛ぶものとする。また必要があれば、この冊子の5ページと6ページの三角関数表を用いよ。
は飛行距離が3%以上短くなることを示せ。ただし地球は完全な球体であるとし、飛行機は高度0を飛ぶものとする。また必要があれば、この冊子の5ページと6ページの三角関数表を用いよ。
注:大円とは、球を球の中心を通る平面で切ったとき、その切り口にできる円のことである。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
三角関数表(1)
| 角 | 正弦(sin) | 余弦(cos) | 正接(tan) |
| 角 | 正弦(sin) | 余弦(cos) | 正接(tan) |
| 0.0° | 0.0000 | 1.0000 | 0.0000 |
| 22.5° | 0.3827 | 0.9239 | 0.4142 |
| 0.5° | 0.0087 | 1.0000 | 0.0087 |
| 23.0° | 0.3907 | 0.9205 | 0.4245 |
| 1.0° | 0.0175 | 0.9998 | 0.0175 |
| 23.5° | 0.3987 | 0.9171 | 0.4348 |
| 1.5° | 0.0262 | 0.9997 | 0.0262 |
| 24.0° | 0.4067 | 0.9135 | 0.4452 |
| 2.0° | 0.0349 | 0.9994 | 0.0349 |
| 24.5° | 0.4147 | 0.9100 | 0.4557 |
| 2.5° | 0.0436 | 0.9990 | 0.0437 |
| 25.0° | 0.4226 | 0.9063 | 0.4663 |
| 3.0° | 0.0523 | 0.9986 | 0.0524 |
| 25.5° | 0.4305 | 0.9026 | 0.4770 |
| 3.5° | 0.0610 | 0.9981 | 0.0612 |
| 26.0° | 0.4384 | 0.8988 | 0.4877 |
| 4.0° | 0.0698 | 0.9976 | 0.0699 |
| 26.5° | 0.4462 | 0.8949 | 0.4986 |
| 4.5° | 0.0785 | 0.9969 | 0.0787 |
| 27.0° | 0.4540 | 0.8910 | 0.5095 |
| 5.0° | 0.0872 | 0.9962 | 0.0875 |
| 27.5° | 0.4617 | 0.8870 | 0.5206 |
| 5.5° | 0.0958 | 0.9954 | 0.0963 |
| 28.0° | 0.4695 | 0.8829 | 0.5317 |
| 6.0° | 0.1045 | 0.9945 | 0.1051 |
| 28.5° | 0.4772 | 0.8788 | 0.5430 |
| 6.5° | 0.1132 | 0.9936 | 0.1139 |
| 29.0° | 0.4848 | 0.8746 | 0.5543 |
| 7.0° | 0.1219 | 0.9925 | 0.1228 |
| 29.5° | 0.4924 | 0.8704 | 0.5658 |
| 7.5° | 0.1305 | 0.9914 | 0.1317 |
| 30.0° | 0.5000 | 0.8660 | 0.5774 |
| 8.0° | 0.1392 | 0.9903 | 0.1405 |
| 30.5° | 0.5075 | 0.8616 | 0.5890 |
| 8.5° | 0.1478 | 0.9890 | 0.1495 |
| 31.0° | 0.5150 | 0.8572 | 0.6009 |
| 9.0° | 0.1564 | 0.9877 | 0.1584 |
| 31.5° | 0.5225 | 0.8526 | 0.6128 |
| 9.5° | 0.1650 | 0.9863 | 0.1673 |
| 32.0° | 0.5299 | 0.8480 | 0.6249 |
| 10.0° | 0.1736 | 0.9848 | 0.1763 |
| 32.5° | 0.5373 | 0.8434 | 0.6371 |
| 10.5° | 0.1822 | 0.9833 | 0.1853 |
| 33.0° | 0.5446 | 0.8387 | 0.6494 |
| 11.0° | 0.1908 | 0.9816 | 0.1944 |
| 33.5° | 0.5519 | 0.8339 | 0.6619 |
| 11.5° | 0.1994 | 0.9799 | 0.2035 |
| 34.0° | 0.5592 | 0.8290 | 0.6745 |
| 12.0° | 0.2079 | 0.9781 | 0.2126 |
| 34.5° | 0.5664 | 0.8241 | 0.6873 |
| 12.5° | 0.2164 | 0.9763 | 0.2217 |
| 35.0° | 0.5736 | 0.8192 | 0.7002 |
| 13.0° | 0.2250 | 0.9744 | 0.2309 |
| 35.5° | 0.5807 | 0.8141 | 0.7133 |
| 13.5° | 0.2334 | 0.9724 | 0.2401 |
| 36.0° | 0.5878 | 0.8090 | 0.7265 |
| 14.0° | 0.2419 | 0.9703 | 0.2493 |
| 36.5° | 0.5948 | 0.8039 | 0.7400 |
| 14.5° | 0.2504 | 0.9681 | 0.2586 |
| 37.0° | 0.6018 | 0.7986 | 0.7536 |
| 15.0° | 0.2588 | 0.9659 | 0.2679 |
| 37.5° | 0.6088 | 0.7934 | 0.7673 |
| 15.5° | 0.2672 | 0.9636 | 0.2773 |
| 38.0° | 0.6157 | 0.7880 | 0.7813 |
| 16.0° | 0.2756 | 0.9613 | 0.2867 |
| 38.5° | 0.6225 | 0.7826 | 0.7954 |
| 16.5° | 0.2840 | 0.9588 | 0.2962 |
| 39.0° | 0.6293 | 0.7771 | 0.8098 |
| 17.0° | 0.2924 | 0.9563 | 0.3057 |
| 39.5° | 0.6361 | 0.7716 | 0.8243 |
| 17.5° | 0.3007 | 0.9537 | 0.3153 |
| 40.0° | 0.6428 | 0.7660 | 0.8391 |
| 18.0° | 0.3090 | 0.9511 | 0.3249 |
| 40.5° | 0.6494 | 0.7604 | 0.8541 |
| 18.5° | 0.3173 | 0.9483 | 0.3346 |
| 41.0° | 0.6561 | 0.7547 | 0.8693 |
| 19.0° | 0.3256 | 0.9455 | 0.3443 |
| 41.5° | 0.6626 | 0.7490 | 0.8847 |
| 19.5° | 0.3338 | 0.9426 | 0.3541 |
| 42.0° | 0.6691 | 0.7431 | 0.9004 |
| 20.0° | 0.3420 | 0.9397 | 0.3640 |
| 42.5° | 0.6756 | 0.7373 | 0.9163 |
| 20.5° | 0.3502 | 0.9367 | 0.3739 |
| 43.0° | 0.6820 | 0.7314 | 0.9325 |
| 21.0° | 0.3584 | 0.9336 | 0.3839 |
| 43.5° | 0.6884 | 0.7254 | 0.9490 |
| 21.5° | 0.3665 | 0.9304 | 0.3939 |
| 44.0° | 0.6947 | 0.7193 | 0.9657 |
| 22.0° | 0.3746 | 0.9272 | 0.4040 |
| 44.5° | 0.7009 | 0.7133 | 0.9827 |
| 22.5° | 0.3827 | 0.9239 | 0.4142 |
| 45.0° | 0.7071 | 0.7071 | 1.0000 |
三角関数表(2)
| 角 | 正弦(sin) | 余弦(cos) | 正接(tan) |
| 角 | 正弦(sin) | 余弦(cos) | 正接(tan) |
| 45.0° | 0.7071 | 0.7071 | 1.0000 |
| 67.5° | 0.9239 | 0.3827 | 2.4142 |
| 45.5° | 0.7133 | 0.7009 | 1.0176 |
| 68.0° | 0.9272 | 0.3746 | 2.4751 |
| 46.0° | 0.7193 | 0.6947 | 1.0355 |
| 68.5° | 0.9304 | 0.3665 | 2.5386 |
| 46.5° | 0.7254 | 0.6884 | 1.0538 |
| 69.0° | 0.9336 | 0.3584 | 2.6051 |
| 47.0° | 0.7314 | 0.6820 | 1.0724 |
| 69.5° | 0.9367 | 0.3502 | 2.6746 |
| 47.5° | 0.7373 | 0.6756 | 1.0913 |
| 70.0° | 0.9397 | 0.3420 | 2.7475 |
| 48.0° | 0.7431 | 0.6691 | 1.1106 |
| 70.5° | 0.9426 | 0.3338 | 2.8239 |
| 48.5° | 0.7490 | 0.6626 | 1.1303 |
| 71.0° | 0.9455 | 0.3256 | 2.9042 |
| 49.0° | 0.7547 | 0.6561 | 1.1504 |
| 71.5° | 0.9483 | 0.3173 | 2.9887 |
| 49.5° | 0.7604 | 0.6494 | 1.1708 |
| 72.0° | 0.9511 | 0.3090 | 3.0777 |
| 50.0° | 0.7660 | 0.6428 | 1.1918 |
| 72.5° | 0.9537 | 0.3007 | 3.1716 |
| 50.5° | 0.7716 | 0.6361 | 1.2131 |
| 73.0° | 0.9563 | 0.2924 | 3.2709 |
| 51.0° | 0.7771 | 0.6293 | 1.2349 |
| 73.5° | 0.9588 | 0.2840 | 3.3759 |
| 51.5° | 0.7826 | 0.6225 | 1.2572 |
| 74.0° | 0.9613 | 0.2756 | 3.4874 |
| 52.0° | 0.7880 | 0.6157 | 1.2799 |
| 74.5° | 0.9636 | 0.2672 | 3.6059 |
| 52.5° | 0.7934 | 0.6088 | 1.3032 |
| 75.0° | 0.9659 | 0.2588 | 3.7321 |
| 53.0° | 0.7986 | 0.6018 | 1.3270 |
| 75.5° | 0.9681 | 0.2504 | 3.8667 |
| 53.5° | 0.8039 | 0.5948 | 1.3514 |
| 76.0° | 0.9703 | 0.2419 | 4.0108 |
| 54.0° | 0.8090 | 0.5878 | 1.3764 |
| 76.5° | 0.9724 | 0.2334 | 4.1653 |
| 54.5° | 0.8141 | 0.5807 | 1.4019 |
| 77.0° | 0.9744 | 0.2250 | 4.3315 |
| 55.0° | 0.8192 | 0.5736 | 1.4281 |
| 77.5° | 0.9763 | 0.2164 | 4.5107 |
| 55.5° | 0.8241 | 0.5664 | 1.4550 |
| 78.0° | 0.9781 | 0.2079 | 4.7046 |
| 56.0° | 0.8290 | 0.5592 | 1.4826 |
| 78.5° | 0.9799 | 0.1994 | 4.9152 |
| 56.5° | 0.8339 | 0.5519 | 1.5108 |
| 79.0° | 0.9816 | 0.1908 | 5.1446 |
| 57.0° | 0.8387 | 0.5446 | 1.5399 |
| 79.5° | 0.9833 | 0.1822 | 5.3955 |
| 57.5° | 0.8434 | 0.5373 | 1.5697 |
| 80.0° | 0.9848 | 0.1736 | 5.6713 |
| 58.0° | 0.8480 | 0.5299 | 1.6003 |
| 80.5° | 0.9863 | 0.1650 | 5.9758 |
| 58.5° | 0.8526 | 0.5225 | 1.6319 |
| 81.0° | 0.9877 | 0.1564 | 6.3138 |
| 59.0° | 0.8572 | 0.5150 | 1.6643 |
| 81.5° | 0.9890 | 0.1478 | 6.6912 |
| 59.5° | 0.8616 | 0.5075 | 1.6977 |
| 82.0° | 0.9903 | 0.1392 | 7.1154 |
| 60.0° | 0.8660 | 0.5000 | 1.7321 |
| 82.5° | 0.9914 | 0.1305 | 7.5958 |
| 60.5° | 0.8704 | 0.4924 | 1.7675 |
| 83.0° | 0.9925 | 0.1219 | 8.1443 |
| 61.0° | 0.8746 | 0.4848 | 1.8040 |
| 83.5° | 0.9936 | 0.1132 | 8.7769 |
| 61.5° | 0.8788 | 0.4772 | 1.8418 |
| 84.0° | 0.9945 | 0.1045 | 9.5144 |
| 62.0° | 0.8829 | 0.4695 | 1.8807 |
| 84.5° | 0.9954 | 0.0958 | 10.385 |
| 62.5° | 0.8870 | 0.4617 | 1.9210 |
| 85.0° | 0.9962 | 0.0872 | 11.430 |
| 63.0° | 0.8910 | 0.4540 | 1.9626 |
| 85.5° | 0.9969 | 0.0785 | 12.706 |
| 63.5° | 0.8949 | 0.4462 | 2.0057 |
| 86.0° | 0.9976 | 0.0698 | 14.301 |
| 64.0° | 0.8988 | 0.4384 | 2.0503 |
| 86.5° | 0.9981 | 0.0610 | 16.350 |
| 64.5° | 0.9026 | 0.4305 | 2.0965 |
| 87.0° | 0.9986 | 0.0523 | 19.081 |
| 65.0° | 0.9063 | 0.4226 | 2.1445 |
| 87.5° | 0.9990 | 0.0436 | 22.904 |
| 65.5° | 0.9100 | 0.4147 | 2.1943 |
| 88.0° | 0.9994 | 0.0349 | 28.636 |
| 66.0° | 0.9135 | 0.4067 | 2.2460 |
| 88.5° | 0.9997 | 0.0262 | 38.188 |
| 66.5° | 0.9171 | 0.3987 | 2.2998 |
| 89.0° | 0.9998 | 0.0175 | 57.290 |
| 67.0° | 0.9205 | 0.3907 | 2.3559 |
| 89.5° | 1.0000 | 0.0087 | 114.59 |
| 67.5° | 0.9239 | 0.3827 | 2.4142 |
| 90.0° | 1.0000 | 0.0000 | ------ |
解答 実質的に甲[6]の問題と同一問題です。
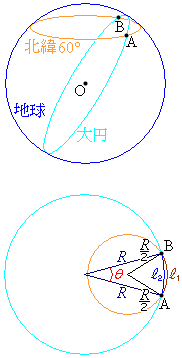
地球の半径をRとします。
北緯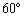 で地球を切った切り口の円(右図で橙色の円)を
で地球を切った切り口の円(右図で橙色の円)を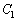 とします。地球上の2点A,Bはいずれも北緯
とします。地球上の2点A,Bはいずれも北緯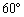 なので、
なので、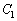 上の点です。また、
上の点です。また、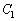 の半径は、
の半径は、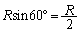 です。
です。
A,Bを通る大円を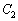 とします。A,Bは当然
とします。A,Bは当然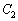 上の点です。また、地球の中心を通る平面で切った切り口の円(右図で水色の円)なので、
上の点です。また、地球の中心を通る平面で切った切り口の円(右図で水色の円)なので、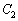 の半径はRです。
の半径はRです。
右下図のように、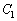 ,
,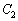 をA,Bで交差させるように同一平面上に描けば、
をA,Bで交差させるように同一平面上に描けば、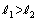 は明らかです。
は明らかです。
地軸(北極と南極を結ぶ線分)と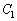 を含む平面との交点をPとして、
を含む平面との交点をPとして、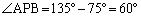 より、
より、
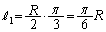 (弧長の公式は、一般角を参照)
(弧長の公式は、一般角を参照) 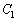 の半径に等しく
の半径に等しく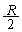 です。
です。
地球の中心をOとして、∠AOB=θ とおくと、θ は鋭角で、三角形AOBにおいて余弦定理より、
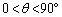 であって、三角関数表で、
であって、三角関数表で、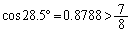 ,
,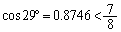 より、
より、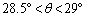 ,
,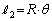 より、
より、
よって、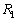 に比べて
に比べて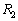 は飛行距離が3%以上短くなります。
は飛行距離が3%以上短くなります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。