京都大学理系2008年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
甲[1] 直線 が関数
が関数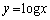 のグラフと共有点を持たないためにpとqが満たすべき必要十分条件を求めよ。
のグラフと共有点を持たないためにpとqが満たすべき必要十分条件を求めよ。
[解答へ]
甲[2] 正四面体ABCDを考える。点Pは時刻0では頂点Aに位置し、1秒ごとにある頂点から他の3頂点のいずれかに、等しい確率で動くとする。このとき、時刻0から時刻nまでの間に、4頂点A,B,C,Dのすべてに点Pが現れる確率を求めよ。ただしnは1以上の正数とする。
[解答へ]
甲[3] AB=ACである二等辺三角形ABCを考える。辺ABの中点をMとし、辺ABを延長した直線上に点Nを、AN:NB=2:1となるようにとる。このとき∠BCM=∠BCNとなることを示せ。ただし、点Nは辺AB上にはないものとする。
[解答へ]
甲[4] 定数aは実数であるとする。方程式
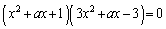
を満たす実数xはいくつあるか。aの値によって分類せよ。
[解答へ]
甲[5] 次の式で与えられる底面の半径が2,高さが1の円柱Cを考える。
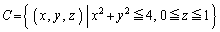
xy平面上の直線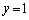 を含み、xy平面と
を含み、xy平面と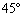 の角をなす平面のうち、点
の角をなす平面のうち、点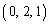 を通るものをHとする。円柱Cを平面Hで二つに分けるとき、点
を通るものをHとする。円柱Cを平面Hで二つに分けるとき、点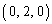 を含む方の体積を求めよ。
を含む方の体積を求めよ。
[解答へ]
甲[6] 空間内に原点Oを中心とした半径1の球面Sを考え、S上の2点をA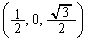 ,B
,B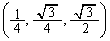 とする。
とする。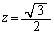 で与えられる平面でSを切った切り口の円において、AとBを結ぶ弧のうち短い方の長さを
で与えられる平面でSを切った切り口の円において、AとBを結ぶ弧のうち短い方の長さを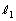 とする。また3点O,A,Bを通る平面でSを切った切り口の円において、AとBを結ぶ弧のうち短い方の長さを
とする。また3点O,A,Bを通る平面でSを切った切り口の円において、AとBを結ぶ弧のうち短い方の長さを とする。このとき
とする。このとき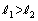 を証明せよ。
を証明せよ。
[解答へ]
乙[1]
甲[1]と同一
乙[2]
甲[2]と同一
乙[3] 空間の1点Oを通る4直線で、どの3直線も同一平面上にないようなものを考える。このとき、4直線のいずれともO以外の点で交わる平面で、4つの交点が平行四辺形の頂点になるようなものが存在することを示せ。
[解答へ]
乙[4] 定数aは実数であるとする。関数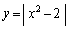 と
と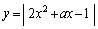 のグラフの共有点はいくつあるか。aの値によって分類せよ。
のグラフの共有点はいくつあるか。aの値によって分類せよ。
[解答へ]
乙[5]
甲[5]と同一
乙[6]
地球上の北緯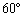 東経
東経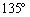 の地点をA,北緯
の地点をA,北緯 東経
東経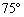 の地点をBとする。AからBに向かう2種類の飛行経路
の地点をBとする。AからBに向かう2種類の飛行経路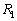 ,
,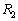 を考える。
を考える。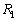 は西に向かって同一緯度で飛ぶ経路とする。
は西に向かって同一緯度で飛ぶ経路とする。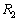 は地球の大円に沿った経路のうち飛行距離の短い方とする。
は地球の大円に沿った経路のうち飛行距離の短い方とする。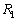 に比べて
に比べて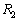 は飛行距離が3%以上短くなることを示せ。ただし地球は完全な球体であるとし、飛行機は高度0を飛ぶものとする。また必要があれば、この冊子の5ページと6ページの三角関数表を用いよ。
は飛行距離が3%以上短くなることを示せ。ただし地球は完全な球体であるとし、飛行機は高度0を飛ぶものとする。また必要があれば、この冊子の5ページと6ページの三角関数表を用いよ。
注:大円とは、球を球の中心を通る平面で切ったとき、その切り口にできる円のことである。
[解答へ] (注.三角関数表は解答ページにあります)
各問検討
甲[1](解答はこちら) 素直な受験生は、この問題を、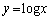 のグラフと直線
のグラフと直線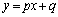 の位置関係から考えると思います。
の位置関係から考えると思います。
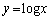 は単調増加で
は単調増加で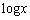 は全実数をとります。
は全実数をとります。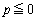 であれば、単調減少もしくは定数値をとる
であれば、単調減少もしくは定数値をとる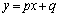 と、
と、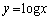 は必ず交点をもってしまうので、
は必ず交点をもってしまうので、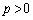 のときは、
のときは、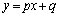 と
と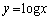 が接するところを求めるために、
が接するところを求めるために、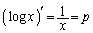 として、
として、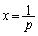
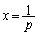 のとき、
のとき、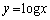 のy座標は、
のy座標は、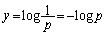
直線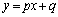 が
が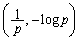 よりも上を通過すれば、
よりも上を通過すれば、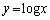 と共有点をもたないから、
と共有点をもたないから、
∴ 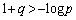
というようにしてくれば、試験会場でも充分に実用的です。
ですが、入試問題は問題文に書かれているとおりに考えなければいけないというものではありません。別の角度から眺めることにより、難問が平凡な問題に変わってしまう、ということはよくあることです。
「定数の分離」という受験技巧がありますが、
定数だけ=xを含む式 ・・・(*)
という形にすると問題を捉えやすくなるのです(微分法の方程式への応用(2)を参照)。
そこで、解答では、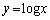 と
と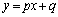 を連立して、
を連立して、
(*)の形を作るために、定数qを分離して、
として、関数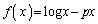 を考えました。
を考えました。
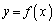 のグラフを描き、x軸に平行な直線
のグラフを描き、x軸に平行な直線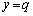 がqの値によってどの辺を通るか、ということを考えれば、
がqの値によってどの辺を通るか、ということを考えれば、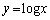 と
と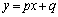 の共有点について調べることができます。
の共有点について調べることができます。
「定数の分離」は応用範囲の広い技巧なので、すぐに思いつけるようにしておいてください。
甲[2](解答はこちら) 正攻法で、A,B,C,Dの4文字から1文字ずつ選んで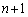 個の文字を並べるのに、一番最初をAとして、同じ文字が隣接しないような並べ方を数える、というような考え方では難しいでしょう。確率・場合の数では、正攻法で難しければ「余事象」が切り札になります。
個の文字を並べるのに、一番最初をAとして、同じ文字が隣接しないような並べ方を数える、というような考え方では難しいでしょう。確率・場合の数では、正攻法で難しければ「余事象」が切り札になります。
「4頂点すべてに点Pが現れる」という事象の余事象ということになれば、4頂点のうち2頂点にしかPが来ない、または、4頂点のうち3頂点にしかPが来ない、ということになります。
2頂点に来るのは、Aともう一つの頂点を往復する場合です。確率はすぐに求められます。
3頂点に来る場合が問題ですが、例えば、A,B,Cの3頂点の中だけで動く場合の確率から、2頂点を往復する(既に求めている)場合の確率を引けばよいので、何とかなりそうです。
こうした確率の問題、特に、あまり難問とは言えないような問題で注意しなければいけないのは、思わぬミスです。重複カウントや場合分け忘れなどの勘違いで不覚をとることのないように気をつける必要があります。必ず、nの小さな場合などで、確認をするように心がけてください。
甲[3](解答はこちら) こういう平面幾何の問題で意表をつかれて戸惑った受験生もいたかも知れません。
∠BCM=∠BCNというのは、BCが∠MCNの2等分線ということなので、
MC:CN=MB:BN=1:2
が言えれば良いわけです。ACの中点Pをとって、PB // CNに気づけば、PB:CN=1:2となるので、あとは、PB=MCが言えればよいことになります。
京大では、平面幾何の一部が高校に移ってくる以前から、平面幾何の利用によって簡単に解ける問題が出ていました。こうした問題が出題されるということは、京大入試では、平面幾何の知識が今後も役立つ、ということが言えるだろうと思います。
甲[4](解答はこちら) 展開して4次方程式にしてしまうのでは骨が折れます。定数aを分離するのも無理なことをすればできなくはありませんが、2つの2次方程式にしてしまう方がラクにすみます。ただ、2つの2次方程式が同じ解をもってしまう場合があるので、共通解があるかどうかを別に調べなければいけません。
最近、共通解の問題もあまり見かけません。解答に書いておいた共通解の技巧はポピュラーな技巧とは言えませんが、一応、見ておいてください。例えば、次のような問題で効果があります。
早大理工'86年[4]:
実数a,bは、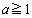 ,
,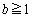 を満たすとする。このとき、つぎの二つの方程式
を満たすとする。このとき、つぎの二つの方程式 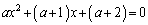 ・・・(i)
・・・(i)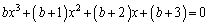 ・・・(ii)
・・・(ii)は共通解を持たないことを示せ。
なお、定数の分離の技巧を無理に使う解法については(私ならやりませんが)、旺文社全国大学入試問題正解に掲載されいるので、興味のある方は参照してください。共通解の探し方も、この本にもう少し簡単にすむ方法が書いてあります。
甲[5](解答はこちら) どんな問題集にも出ていて、理工系の受験生であれば一度は目にしたことがあるだろうという問題です。立体をy軸に垂直な平面で切った断面の面積をy軸方向に積分すればよい、ということは理工系の受験生であれば誰でも知っているはずのことです。問題そのものは標準問題なのですが、正答率が高いか、というとそういうものではありません。計算問題であるがゆえに、ケアレスが入り込みやすく、こういう問題の正答率は意外に低いものなのです。
これから微分・積分を極めよう、という皆さんに申し上げておくと、立体の切断面を考えるときは、その面積を求めやすい方向から立体を切ります。この問題では、y軸に垂直に切ります。切断面は長方形になるので、面積を求めるためには、縦と横の長さを、切断面のy座標kで表します。縦と横の長さを求めるためには、立体を真上から眺めたり、x軸に平行に眺めたりします。それぞれ、どのように見えるのか、図示して考えるようにしましょう。
定積分は、断面積を、立体が存在するy座標の範囲について積分します。
定積分は2つの部分に分けられます。
片方は、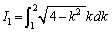 という積分です。この積分は、
という積分です。この積分は、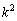 を含む式
を含む式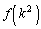 に
に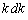 がついているという形:
がついているという形: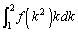 をしています。この場合は、通常、
をしています。この場合は、通常、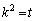 という置換をしますが、これでは、
という置換をしますが、これでは、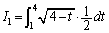 となり、根号内が
となり、根号内が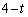 となっておもしろくないのです。そこで、
となっておもしろくないのです。そこで、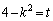 とおけば、
とおけば、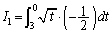 となって、計算しやすくなります。解答では、
となって、計算しやすくなります。解答では、 の積分よりももっとラクにしようということで、根号全体
の積分よりももっとラクにしようということで、根号全体 をtと置きました。できる限り計算ミスをしにくいような計算法を心がけてください。
をtと置きました。できる限り計算ミスをしにくいような計算法を心がけてください。
もう一方は、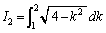 という積分です。この積分は、
という積分です。この積分は、 という置換をするのが定石です。
という置換をするのが定石です。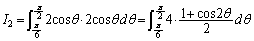 というようにしても積分できますが、解答のように、
というようにしても積分できますが、解答のように、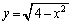 (2乗してみてください)は、円:
(2乗してみてください)は、円: の
の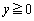 の部分を表すので、円の面積の一部として暗算で求めてしまえば早くすみます。
の部分を表すので、円の面積の一部として暗算で求めてしまえば早くすみます。
こういう計算問題は、誰がやってもミスをし易いものです。計算ミスをしたからと言って、自分を責めたりしないようにしましょう。何が大切かと言うと、誰でもミスはするものだ、ということを認めて、しっかりと検算することです。検算も、計算をした直後に行うと、脳内が沸騰していて、検算時にまた同じミスをやるので、一旦、他の問題に飛んで、計算過程を忘れてから見直すようにするとミスを発見し易くなります。
甲[6](解答はこちら) 球面上で2点間の経路の長さを比べる問題で、やりにくそうに見えますが、「空間図形の問題は平面図形に置き直して考える」ということを一つの定石としてください。この問題では、解答のように、問題文に出てくる2円をA,Bで交差するように同一平面上に描いてしまえば、2経路の大小は一見して明らかです。
半径の小さい方の円周上の長さの方が大きい、としても、多分、許してもらえると思いますが、解答では実際に長さを比べてあります。
2円の半径は、片方が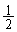 で、もう一方が1になります。
で、もう一方が1になります。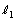 と
と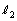 の長さを求めるために、
の長さを求めるために、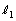 を見込む中心角φ,
を見込む中心角φ,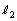 を見込む中心角θ を考えます。φは正三角形の頂角になるので
を見込む中心角θ を考えます。φは正三角形の頂角になるので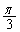 とわかります。θ は、余弦定理で求めますが、
とわかります。θ は、余弦定理で求めますが、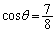 としかわかりません。
としかわかりません。
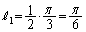 ,
,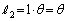
を比べなければいけませんが、θ がわからないので、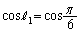 と
と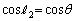 を比べることになります。
を比べることになります。
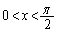 において、
において、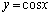 は単調減少関数なので、
は単調減少関数なので、 より、
より、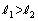
というストーリーになります。
いわゆる受験技巧が通用しない問題、ということで、理工系の全受験生に考えて頂きたい良問だと思います。
乙[3](解答はこちら) 京大は、「条件・・・をみたす・・・が存在することを示せ」という問題をよく出題します。「必ずA⇒Bとなること」を示すのに比べて、「存在」を示す問題は、全部のものが条件をみたすわけではないけれど、中に条件をみたすものが存在することを示す、という点で、示し方が難しくなります。
条件(C)をみたすものが存在するなら、それは条件(D)をみたすはずだ、というのでは、存在を示したことにはなりません。条件(D)をみたすものはどんなものか、本当に存在するのか、ということを言わなければいけません。
これをできるだけ簡単に考えるためには、条件(C)をみたすものを見つけ出す方法を説明すればよいのです。「天竺の国には不老長寿の薬が存在することを示せ」と言うのであれば、天竺の国に行く行き方を示し、こうすれば必ず不老長寿の薬を手に入れることができる、ということを説明すれば、「存在」を示したことになります。
このとき、不老長寿の薬が実は100種類くらいあるとして、100種類のうち1種類の入手法を説明すれば、「存在」を示したことになります。100種類すべての入手法を説明する必要はありません。
「4直線との交点が平行四辺形の4頂点となるような平面が存在することを示せ」というのであれば、平面と4直線との交点を4頂点とするような四角形でいて、平行四辺形となるものを、どうやって見つけることができるのか、ということを説明します。
解答では、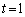 ,
,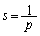 ,
,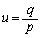 ,
,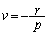 となるように、s,t,u,vを定めて、4直線上の点A(
となるように、s,t,u,vを定めて、4直線上の点A(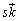 ),B(
),B(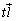 ),C(
),C(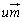 ),D(
),D(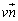 )をとれば、
)をとれば、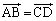 となっていて、四角形ABDCが平行四辺形になっていることを説明しました。
となっていて、四角形ABDCが平行四辺形になっていることを説明しました。
4直線との交点が平行四辺形となるようなものの見つけ方が説明されているので、条件を満たす平面の「存在」が示せたことになります。
乙[4](解答はこちら) この問題は、式変形により、'08年前期甲[4]に帰着します。甲[4]の検討を参照してください。
乙[6](解答はこちら) 実質的に'08年前期甲[6]と同じ問題ですが、三角関数の表がついていて、数値計算をするようになっています。
詳細な三角関数の表にはびっくりしますが、昨年、東工大'07年物理前期[3]でも出ているので、京大の先生が、じゃあうちでも、と、思ったのかも知れません。
球面上で考え抽象的で目的のわからない甲[6]と比べて、地球表面の飛行距離をイメージして具体的で問題の目的が明確な乙[6]の方が取り組みやすいのではないかと私は思うのですが......。
緯度・経度がわからない、という受験生がいたそうです。三角関数表よりもこの方が私には驚きでした。京大に合格したとして、卒業後、気象を扱うような仕事についたときに、台風や低気圧の進路をどう考えるつもりなのでしょうか?入試の範囲以外のことは関係ない、と言うのなら、京都大学を目指すべきではないと私は思います。こちらをご覧の皆さんには、ぜひ幅広い素養を身につけるように頑張って頂きたいと思います。
同一緯度上の経路と大円上の経路との大小は直感的にわかると思うので、三角関数の表が与えられていて、経路の長さを数値的に比較できる、という点でも、乙[6]は、角の大きさで比較できない甲[6]よりやりやすいと言えるのではないでしょうか。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。