���嗝�n���w'08�N��[4]
�萔a�͎����ł���Ƃ���B��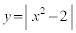 ��
��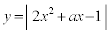 �̃O���t�̋��L�_�͂������邩�Ba�̒l�ɂ���ĕ��ނ���B
�̃O���t�̋��L�_�͂������邩�Ba�̒l�ɂ���ĕ��ނ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ό`�ɂ���b[4]�̖��ɋA�����܂��B
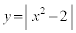 �@����@
�@����@
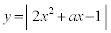 �@����A
�@����A
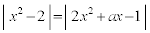 ��
�� 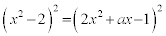
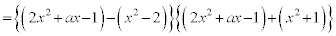
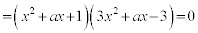 �@����B
�@����B�� 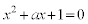 �@����C�@�܂��́A
�@����C�@�܂��́A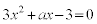 �@����D
�@����D 2���������C�̔��ʎ��F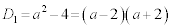 �@
�@
2���������D�̔��ʎ��F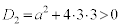 �@
�@
2���������C�́A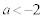 �C
�C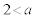 �̂Ƃ��ɁA���قȂ�2�������A
�̂Ƃ��ɁA���قȂ�2�������A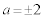 �̂Ƃ��Ɏ����̏d���������A
�̂Ƃ��Ɏ����̏d���������A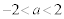 �̂Ƃ��ɂ͎������������܂���(2���������̈�ʘ_���Q��)�B
�̂Ƃ��ɂ͎������������܂���(2���������̈�ʘ_���Q��)�B
2���������D�́Aa�̒l�ɂ�����炸�A���قȂ�2�������������܂��B
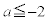 �C
�C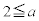 �̏ꍇ�ɁA�B�C�D�ɋ��ʉ������邩�ǂ������ׂ܂��B
�̏ꍇ�ɁA�B�C�D�ɋ��ʉ������邩�ǂ������ׂ܂��B
�C�~3�|�D�Ƃ��āA
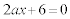 ��
�� 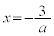
�C�ɑ������ƁA
(i) 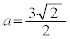 �̂Ƃ��A
�̂Ƃ��A �C�F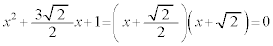
�D�F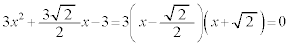
����āA�B�́A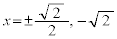 ��3�������������܂��B
��3�������������܂��B (ii) 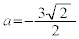 �̂Ƃ��A
�̂Ƃ��A �C�F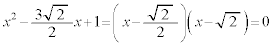
�D�F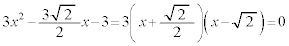
����āA�B�́A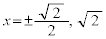 ��3�������������܂��B
��3�������������܂��B (i)�C(ii)�ȊO��a�ɂ��ẮA�C�C�D�����ʉ��������Ƃ͂���܂���B
�ȏ���A�@�C�A�̃O���t�̋��L�_�̌��́A
�E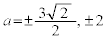 �̂Ƃ��A3��
�̂Ƃ��A3�� �E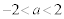 �̂Ƃ��A2�� ......[��]
�̂Ƃ��A2�� ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B