���嗝�n���w'08�N��[3]
��Ԃ�1�_O��ʂ�4�����ŁA�ǂ�3���������ꕽ�ʏ�ɂȂ��悤�Ȃ��̂��l����B���̂Ƃ��A4�����̂�����Ƃ�O�ȊO�̓_�Ō���镽�ʂŁA4�̌�_�����s�l�ӌ`�̒��_�ɂȂ�悤�Ȃ��̂����݂��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�x�N�g���ōl����̂����N�ł��B�u���݂���v���Ƃ��������߂ɂ́A�����ɍ������̂����߂���@��������܂��B�����ł́A���s�l�ӌ`�̋��ߕ����������A�u���݂���v���Ƃ����������ƂɂȂ�܂��B�Ȃ��A�����̃x�N�g���������A��ԃx�N�g�����Q�Ƃ��Ă��������B
O�����_�Ƃ��A4�����̕����x�N�g����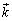 �C
�C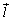 �C
�C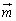 �C
�C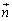 �Ƃ��܂��B
�Ƃ��܂��B
�܂��A4������̓_���AA(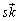 )�CB(
)�CB(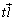 )�CC(
)�CC(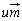 )�CD(
)�CD(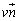 )�Ƃ��܂�(�����ł���̂́A4�����Ƃ��_O��ʂ邩��ł�)�B
)�Ƃ��܂�(�����ł���̂́A4�����Ƃ��_O��ʂ邩��ł�)�B
�ǂ�3���������ꕽ�ʏ�ɑ��݂��Ȃ��̂ŁA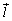 �C
�C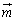 �C
�C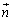 ��3�x�N�g����1���Ɨ��ŁA
��3�x�N�g����1���Ɨ��ŁA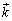 ���A0�ł͂Ȃ�3�̎����̒萔p�Cq�Cr��p���āA
���A0�ł͂Ȃ�3�̎����̒萔p�Cq�Cr��p���āA
�ƕ\�����Ƃ��ł��܂��B
���D�Ⴆ��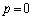 ���Ƃ���ƁA
���Ƃ���ƁA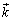 �́A
�́A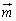 ��
��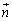 �̍�镽�ʓ��̃x�N�g���ɂȂ�A
�̍�镽�ʓ��̃x�N�g���ɂȂ�A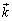 �C
�C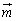 �C
�C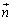 ������x�N�g���Ƃ���3�����͓��ꕽ�ʏ�̒����ɂȂ��Ă��܂��܂��B
������x�N�g���Ƃ���3�����͓��ꕽ�ʏ�̒����ɂȂ��Ă��܂��܂��B
�����ŁA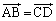 �Ƃ���ƁA
�Ƃ���ƁA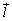 �C
�C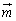 �C
�C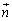 �̌W���ɂ��āA
�̌W���ɂ��āA
���̇@�����������A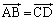 �ƂȂ�̂ŁA�l�p�`ABDC�͕��s�l�ӌ`�ł��B
�ƂȂ�̂ŁA�l�p�`ABDC�͕��s�l�ӌ`�ł��B
��Ԃ�1�_O��ʂ�4�����ŁA�ǂ�3���������ꕽ�ʏ�ɂȂ��悤�Ȃ��̂��^�����A�܂�A3��1���Ɨ��ȃx�N�g��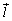 �C
�C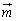 �C
�C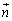 �ƁA3��0�ł͂Ȃ������̒萔p�Cq�Cr�ƁA
�ƁA3��0�ł͂Ȃ������̒萔p�Cq�Cr�ƁA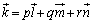 ���^����ꂽ�Ƃ��A
���^����ꂽ�Ƃ��A
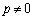 ���A�Ⴆ�·@��p���āA
���A�Ⴆ�·@��p���āA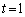 �C
�C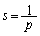 �C
�C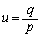 �C
�C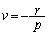 �ƒ�߁A
�ƒ�߁A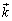 �C
�C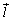 �C
�C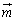 �C
�C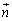 ������x�N�g���Ƃ���4������̓_A(
������x�N�g���Ƃ���4������̓_A(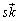 )�CB(
)�CB(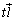 )�CC(
)�CC(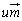 )�CD(
)�CD(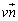 )���Ƃ�܂��Bs�Ct�Cu�Cv�͂������0�ł͂Ȃ��̂ŁAA�CB�CC�CD��O�Ƃ͈قȂ�_�ł��B����ł��Ă��A
)���Ƃ�܂��Bs�Ct�Cu�Cv�͂������0�ł͂Ȃ��̂ŁAA�CB�CC�CD��O�Ƃ͈قȂ�_�ł��B����ł��Ă��A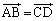 �ƂȂ�A�l�p�`ABDC�����s�l�ӌ`�ɂȂ�܂��B
�ƂȂ�A�l�p�`ABDC�����s�l�ӌ`�ɂȂ�܂��B
���̕��s�l�ӌ`ABDC���܂ޕ��ʂ�I�ׂA
4�����̂�����Ƃ�O�ȊO�̓_�Ō���镽�ʂŁA4�̌�_�����s�l�ӌ`�̒��_�ɂȂ�悤�Ȃ��̂����݂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B