京大理系数学'08年甲[1]
直線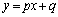
が関数
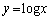のグラフと共有点を持たないためにpとqが満たすべき必要十分条件を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 対数の底はe (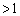
)とします。微分法の方程式への応用を参照してください。
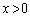において、関数
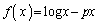を考えると、
直線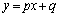
と関数
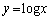のグラフが共有点を持たない ⇔ 直線
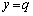と関数
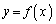のグラフが共有点を持たない
ということになります。
，
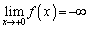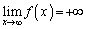より、
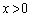において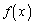
の値は全実数をとります。
従って、qがいかなる実数であっても、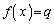
となる正数xが必ず存在し、直線
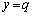と関数
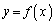のグラフは共有点を持ち、直線
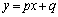と関数
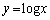のグラフは共有点を持ちます。増減表より、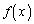
は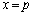
において最大値：
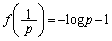を持つ(関数の増減を参照)ので、 ・
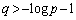であれば、直線
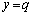と関数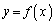
のグラフは共有点を持たず、直線
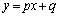と関数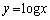
のグラフも共有点を持ちません。 以上より、求める必要十分条件は、
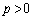，かつ、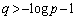
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
のとき、
とすると、
，
であれば、直線
と関数
のグラフは共有点を持ち、
より、
，つまり、
は
