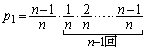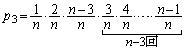京大理系数学'09年乙[3]
n枚のカードを積んだ山があり、各カードには上から順番に1からnまでの番号がつけられている。ただし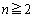
とする。このカードの山に対して次の試行を繰り返す。1回の試行では、一番上のカードを取り、山の一番上にもどすか、あるいはいずれかのカードの下に入れるという操作を行う。これらn通りの操作はすべて同じ確率であるとする。n回の試行を終えたとき、最初一番下にあったカード(番号n)が山の一番上にきている確率を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 試行をn回行うので、すべての試行で番号nのカードが1つ上に上がるのではなく、n回のうち1回だけ上に上がらない試行があること、また、番号nのカードが一番上にあるときとそうでないときとで違いがある(解答では、場合分けして考えます)ことに注意しましょう。以下の解答では、参考までに[．．．]内にピンク色の文字で
，
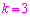の場合を示します。
なお、確率、積事象を参照してください。
・番号nのカードが上からk枚目の位置(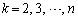
)にあるとき、一番上にあるカードを取ると、番号nの下側では入れる位置が
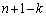通り、番号nのカードの上側では入れる位置が
通りあります。このとき、以下の(i)，(ii)のいずれかの事象が起こります。 (i) 一番上にあったカードが番号nのカードよりも下側に入る事象
この確率は、n通りの位置のうちから
通りの位置のどれか1つの位置を選ぶので、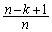
です。このときに、番号nのカードの位置が1つ上になり、上から
枚目の位置にきます。[番号6のカードが上から3番目にあるとき、一番上にあったカードが番号6よりも下側に入る確率は
] (ii) 一番上にあったカードが番号nのカードよりも上側に入る事象。
この確率は
です。このときは、番号nのカードの位置は変わりません。[番号6のカードが上から3番目にあるとき、一番上にあったカードが番号6よりも上側に入る確率は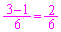
] 第1回目の試行の前に、番号nのカードは上からn番目の位置にいます。[第1回目の試行の前に、番号6のカードは上から6番目にいます]第1回目に事象(i)が起きたとき、第2回目の試行の前に、番号nのカードは上から
番目の位置にいます。[第1回目に事象(i)が起きたとき、第2回目の試行の前に、番号6のカードは上から5番目にいます]第2回目まで連続して事象(i)が起きたとき、第3回目の試行の前に、番号nのカードは上から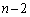
番目の位置にいます。[第2回目まで連続して事象(i)が起きたとき、第3回目の試行の前に、番号6のカードは上から
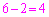番目の位置にいます]第
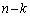回目まで連続して事象(i)が起きたときには、第
回目の試行の前に、番号nのカードは上からk番目の位置にいます。[第
回目まで連続して事象(i)が起きたときには、第
回目の試行の前に、番号6のカードは上から3番目の位置にいます]上記の事象(ii)が起きるのは事象(i)が
回連続した後の第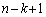
回目です。第
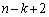回目以降は事象(i)が続いて、起こります。[上記の事象(ii)が起きるのは事象(i)が
回連続した後の第
回目です。第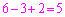
回目以降は事象(i)が続いて、起こります]以下では、第1回目の試行から第
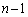回目の試行の間に事象(ii)が起きてしまうときに、n回の試行を終えたとき、番号nのカードが一番上に来る確率を考えます。
第1回目に事象(ii)が起こり、以後
回の試行で連続して事象(i)が起きる確率は、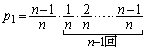 
[
]第1回目に事象(i)が起こり、第2回目に事象(ii)が起こり、以後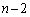
回の試行で連続して事象(i)が起こる確率は、 
[
]第2回目まで連続して事象(i)が起こり、第3回目に事象(ii)が起こり、以後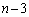
回の試行で連続して事象(i)が起こる確率は、 
[
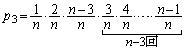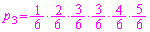]第
回目まで連続して事象(i)が起こり、第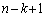
回目に事象(ii)が起こり、以後
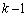回の試行で連続して事象(i)が起こる確率は、 
(
)[
]
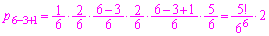・番号nのカードが上から1枚目の位置(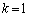
)にあるとき、つまり、第
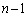回目まで連続して事象(i)が起こり、第n回目の前に番号nのカードが一番上に来ているとき、最終的に番号nのカードが一番上にあるようにするためには、上記とは異なり、第n回目の試行では一番上のカード(番号n)を取って、再び一番上に置く(確率
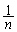)ことになります。この確率は、 
[
]
以上より、求める確率は、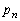
だけが、
，･･･，
と異なる形をしていることに注意して、
(kが2からnまで動くときに
は1から
まで動く)
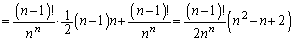......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
