���嗝�n���w'10�N��[5]
���̖₢�ɓ�����B
(1) n�𐳂̐����A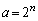 �Ƃ���B
�Ƃ���B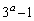 ��
��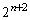 �Ŋ����邪
�Ŋ����邪 �ł͊����Ȃ����Ƃ������B
�ł͊����Ȃ����Ƃ������B (2) m�𐳂̋����Ƃ���B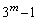 ��
�� �Ŋ�����Ȃ��
�Ŋ�����Ȃ��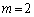 �܂���
�܂��� �ł��邱�Ƃ������B
�ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�́A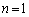 �̂Ƃ�
�̂Ƃ� ��
��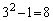 ��
��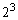 �̔{���A
�̔{���A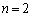 �̂Ƃ���
�̂Ƃ���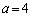 ��
��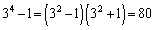 ��
��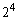 �̔{��(
�̔{��(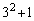 ��2�̔{��)�A
��2�̔{��)�A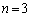 �̂Ƃ���
�̂Ƃ��� ��
��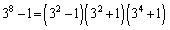 ��
��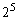 �̔{��(
�̔{��( ��2�̔{��)�A�Ƃ�����ɂȂ��Ă��܂��B
��2�̔{��)�A�Ƃ�����ɂȂ��Ă��܂��B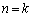 �̏ꍇ����
�̏ꍇ����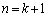 �̏ꍇ�ɍs���Ƃ��ɁA�������������2�̔{�����o�Ă���A�Ƃ����킯�ŁA���w�I�A�[�@�̘g�g�ɏ悹�邱�Ƃ��ł��܂��B�Ȃ��A�������Q�Ƃ��Ă��������B
�̏ꍇ�ɍs���Ƃ��ɁA�������������2�̔{�����o�Ă���A�Ƃ����킯�ŁA���w�I�A�[�@�̘g�g�ɏ悹�邱�Ƃ��ł��܂��B�Ȃ��A�������Q�Ƃ��Ă��������B
(�T) 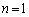 �̂Ƃ��A
�̂Ƃ��A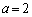 �C
�C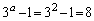 ��
��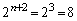 �Ŋ����܂���
�Ŋ����܂���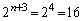 �ł͊����Ȃ��̂ŁA��ӂ͐������܂��B
�ł͊����Ȃ��̂ŁA��ӂ͐������܂��B (�U) 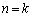 �̂Ƃ��A��ӂ��������A
�̂Ƃ��A��ӂ��������A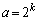 �Ƃ��āA
�Ƃ��āA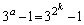 ��
�� �Ŋ����邪
�Ŋ����邪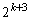 �ł͊����Ȃ��Ɖ��肵�܂��B
�ł͊����Ȃ��Ɖ��肵�܂��B ����ƁAp����Ƃ��āA
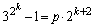 �@����@
�@����@�Ƃ������Ƃ��ł��܂��B
���āA �Ƃ���ƁA
�Ƃ���ƁA p�C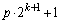 �͊�Ȃ̂ŁA
�͊�Ȃ̂ŁA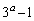 ��
�� �Ŋ����܂���
�Ŋ����܂���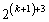 �ł͊����܂���B
�ł͊����܂���B
����āA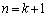 �̂Ƃ�����ӂ͐������܂��B
�̂Ƃ�����ӂ͐������܂��B (�T)�C(�U)���An�𐳂̐����A �Ƃ��āA
�Ƃ��āA ��
�� �Ŋ����邪
�Ŋ����邪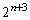 �ł͊����Ȃ����Ƃ�������܂����B
�ł͊����Ȃ����Ƃ�������܂����B
(2) q�𐳂̊�Cn�𐳂̐����Ƃ��āA���̋���m�� �Ƃ��܂��B
�Ƃ��܂��B (1)���A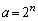 �Ƃ���ƁA
�Ƃ���ƁA ��
��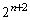 �Ŋ����邪
�Ŋ����邪 �ł͊����Ȃ��̂ŁAp����Ƃ��āA
�ł͊����Ȃ��̂ŁAp����Ƃ��āA �Ƃ������Ƃ��ł��܂��B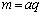 ���A
���A ���J�b�R���́A �C
�C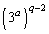 �C����C
�C����C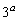 �C1�͂��������ŁA���(q��)�̊�̘a�Ȃ̂Ŋ�ł��Bp�ƒ��J�b�R������Ȃ̂ŁA
�C1�͂��������ŁA���(q��)�̊�̘a�Ȃ̂Ŋ�ł��Bp�ƒ��J�b�R������Ȃ̂ŁA ��
�� �Ŋ����܂���
�Ŋ����܂���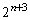 �ł͊����܂���B��ӂ��A
�ł͊����܂���B��ӂ��A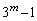 ��
�� �Ŋ�����̂ŁA2�̎w��
�Ŋ�����̂ŁA2�̎w��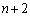 �Cm�Ɋւ��āA
�Cm�Ɋւ��āA 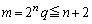 �@����A
�@����A���������܂��B �ɂ����ẮA
�ɂ����ẮA �ł����āAq�͐��̊�Ȃ̂ŁA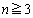 �ł͇A�������̐���n�͑��݂��܂���B�܂��A
�ł͇A�������̐���n�͑��݂��܂���B�܂��A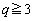 �̂Ƃ��ɂ́A���ׂĂ̐�����n�ɂ���
�̂Ƃ��ɂ́A���ׂĂ̐�����n�ɂ���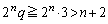 �ƂȂ�A�A�������̐���n�͑��݂��܂���B
�ƂȂ�A�A�������̐���n�͑��݂��܂���B
����āA�A����n�́A �̂Ƃ���
�̂Ƃ��� �݂̂ŁA���̂Ƃ�m�́A
�݂̂ŁA���̂Ƃ�m�́A 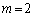 �܂���
�܂���
�Ɍ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B