京大理系数学'11年[6]
空間内に四面体ABCDを考える。このとき、4つの頂点A,B,C,Dを同時に通る球面が存在することを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 京大でよく見かける「......が存在することを示せ」という問題です。考えにくい問題であることが多いのですが、どういう手順で......が求められるか、ということを説明すれば答案を書くことができます。......を求める点順が説明できれば、......は必ず存在するからです。
4つの頂点A,B,C,Dを同時に通る球面が存在するとして、その中心をOとすれば、
OA=OB=OC=OD
となります。従って、4点A,B,C,Dから等距離の点が存在することを言えば、4つの頂点A,B,C,Dを同時に通る球面が存在することが言えます。
まず、三角形ABCを含む平面内で、
OA=OB=OC
を満たす点は、三角形ABCの外心Pです。任意の三角形ABCに対して、外心は必ず存在します。
空間内で、
OA=OB=OC
を満たす点Oは、三角形ABCの外心Pを通り、三角形ABCに垂直な直線l上の点です。
ここで、線分ADの垂直二等分面(ADの中点を通りADに垂直な平面)αを考えます。線分ADの垂直二等分面αが三角形ABCに垂直になることはありません。なぜなら、αが三角形ABCに垂直なとき、点Dは三角形ABCを含む平面上にあって、このとき、四面体ABCDができないからです。
従って、平面αが直線lに平行になることはなく、平面αは直線lと交点をもちます。この交点を改めてOとすると、Oは、平面α上にあるので、
OA=OD
を満たします。このとき、
OA=OB=OC=OD
となり、4点A,B,C,Dから等距離の点Oが存在して、4つの頂点A,B,C,Dを同時に通る球面が存在します。
頂点Aを原点とするような座標系をとり、B,C,Dの位置ベクトルを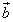 ,
,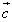 ,
,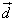 とします。また、4つの頂点A,B,C,Dを同時に通る球面が存在するとして、その中心の位置ベクトルを
とします。また、4つの頂点A,B,C,Dを同時に通る球面が存在するとして、その中心の位置ベクトルを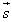 とします。
とします。 より、
よって、
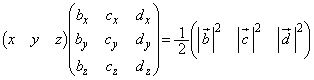 ・・・(*)
・・・(*)の解であるということであって、連立方程式(*)が解を持てば、四面体ABCDに対して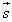 が存在し、4つの頂点A,B,C,Dを同時に通る球面が存在することになります。(*)は、行列
が存在し、4つの頂点A,B,C,Dを同時に通る球面が存在することになります。(*)は、行列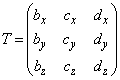 が逆行列
が逆行列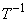 を持てば、(*)の右から
を持てば、(*)の右から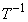 をかけることにより、
をかけることにより、 として解を求めることができます。ここでは四面体ABCDができているので、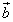 ,
,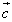 ,
,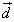 は1次独立で、
は1次独立で、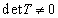 で
で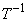 が存在するので、(*)は必ず解を持ちます。
が存在するので、(*)は必ず解を持ちます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 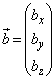 ,
,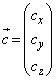 ,
,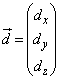 として、
として、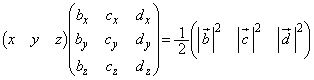 ・・・(*)
・・・(*)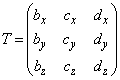 が逆行列
が逆行列