京大理系数学'13年[2]
Nを2以上の自然数とし、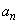 (
(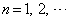 )を次の性質(i),(ii)をみたす数列とする。
)を次の性質(i),(ii)をみたす数列とする。
(i) 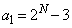 ,
, (ii) 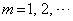 に対して、
に対して、 このときどのような自然数Mに対しても
が成り立つことを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 こうしたイメージのつかみにくい問題では、n,Nに文字を入れて具体的に調べるようにしましょう。本問は、カラクリがつかめてしまえば、大したことはありません。
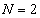 のとき、
のとき、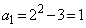 ,
,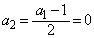 ,以後、
,以後、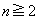 に対して
に対して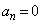 です。
です。
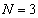 のとき、
のとき、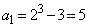 ,
,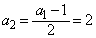 ,
,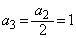 ,
,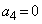 ,以後、
,以後、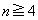 に対して
に対して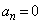 です。
です。
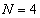 のとき、
のとき、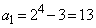 ,
,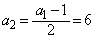 ,
,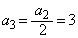 ,
,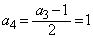 ,
,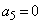 ,以後、
,以後、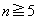 に対して
に対して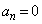 です。
です。
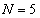 のとき、
のとき、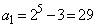 ,
,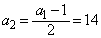 ,
,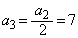 ,
,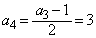 ,
,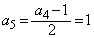 ,
,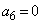 ,以後、
,以後、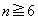 に対して
に対して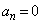 です。
です。
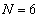 のとき、
のとき、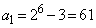 ,
,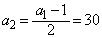 ,
,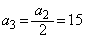 ,
,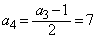 ,
,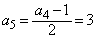 ,
,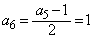 ,
,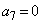 ,以後、
,以後、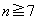 に対して
に対して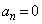 です。
です。
これくらい調べれば、数列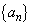 のカラクリがつかめます。
のカラクリがつかめます。
各Nに対して、数列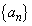 は、はじめの方が異なるだけで、最後の方は同じになります。特に奇数・偶数の並び方は、
は、はじめの方が異なるだけで、最後の方は同じになります。特に奇数・偶数の並び方は、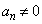 であれば、
であれば、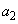 だけが偶数で、それ以外は奇数です。
だけが偶数で、それ以外は奇数です。
そこで、まず、各Nに対して、数列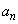 をnを用いて表してみます。最初に
をnを用いて表してみます。最初に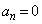 となるnは、上記から
となるnは、上記から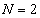 の場合を除いて、
の場合を除いて、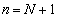 のときです。
のときです。
各Nに対して、各項は、最初の方が自然数で、途中から0になるので、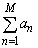 が最大になるのは、
が最大になるのは、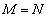 のときです。
のときです。
答案は以下のようになるでしょう。
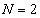 のとき、
のとき、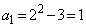 は奇数なので、
は奇数なので、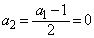 ,以後、
,以後、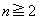 に対して
に対して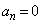
どのような自然数Mに対しても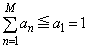 より与不等式は成立する。
より与不等式は成立する。
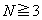 のとき、
のとき、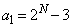 は奇数なので、
は奇数なので、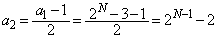 ,
,
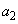 は偶数なので、
は偶数なので、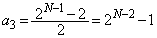
以後、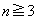 について、
について、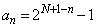 と仮定すると、
と仮定すると、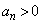 となるのは、
となるのは、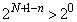 ,つまり、
,つまり、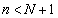 のときで、このとき、
のときで、このとき、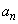 は奇数なので、
は奇数なので、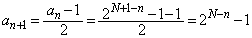
従って、帰納的に、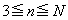 を満たすnについて、
を満たすnについて、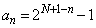 (
(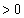 ) (数学的帰納法を参照)
) (数学的帰納法を参照)
特に、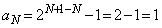 ,よって、
,よって、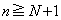 を満たすnについて、
を満たすnについて、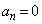
注.つまり、数列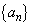 は、最初の2項が、
は、最初の2項が、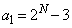 ,
,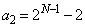 となり、
となり、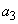
以降は、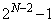 ,・・・,31 (
,・・・,31 (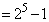 ),15 (
),15 (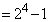 ),7 (
),7 (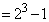 ),3 (
),3 (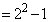 ),1 (
),1 (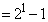 ),0,0,・・・ となっているわけです。
),0,0,・・・ となっているわけです。
以上より、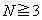 のとき、どのような自然数Mに対しても、
のとき、どのような自然数Mに対しても、
よって、Nを2以上の自然数とするとき、どのような自然数Mに対しても、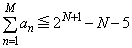 が成り立つ。
が成り立つ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。