�O�p�`�̐��S�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�O�p�`�̊e���_����Εӂɉ��낵��3�{�̐�����1�_�Ō����B���̓_�����S�ƌ����B
�ؖ��@�O�p�`ABC�̒��_A�CB����Ε�BC�CCA�ɐ���AD�CBE�����낵�A��_��H�Ƃ��܂��B
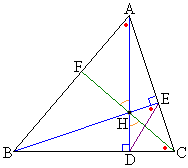 �܂��ACH�̉�����AB�Ƃ̌�_��F�Ƃ��܂��B
�܂��ACH�̉�����AB�Ƃ̌�_��F�Ƃ��܂��B
�l�p�`CEHD�́A ���A�Ό�������p����p���Ȃ��̂ŁA�~�ɓ��ڂ���l�p�`�ł��B
���A�Ό�������p����p���Ȃ��̂ŁA�~�ɓ��ڂ���l�p�`�ł��B
���ꌷDH�̏�ɗ��~���p�͓������̂ŁA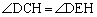 �@����@
�@����@
�܂��A�_D�C�_E�́A�Ƃ��ɁAAB�a�Ƃ���~����̓_�ł��B
���ꌷBD�̏�ɗ��~���p�͓������̂ŁA(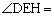 )
)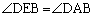 (
(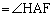 )�@����A
)�@����A
�@�C�A���A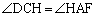
�܂��A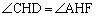 (�Β��p)
(���p)
������A
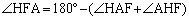
����āA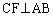
�]���āA�O�p�`�̊e���_����Εӂɉ��낵��3�{�̐�����1�_�Ō����܂��B
(�ؖ��I)
��L���A���ʃx�N�g�����g���Ď������Ƃ��ł��܂��B�O�p�`ABC�̒��_A�CB����Ε�BC�CCA�ɐ��������낵�A��_��H�Ƃ��܂�
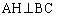 ���A
���A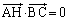 �@(�������Q��)
�@(�������Q��)
�� 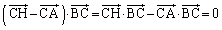 �@����B
�@����B
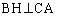 ���A
���A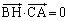
�� 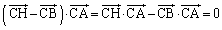 �@����C
�@����C
�B�{�C���A
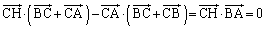
�� 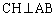
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B