平面ベクトル 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
幾何学の問題を計算処理的アプローチで解決するための道具として、ベクトルを学びます。ベクトルの次元はいくつでも構わないのですが、まず、ベクトルの基本を学ぶために、2次元ベクトル、即ち、平面ベクトルを学びます。
ここで学習する内容は、以下の通りです。各項目をクリックしてください。
ベクトルとは ベクトルとは、AからBに向かう有向線分のことで、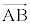
と表します。大きさと向きの両方を考えます。
ベクトルの1次独立 2つのベクトル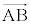
，
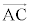が三角形ABCを作るような位置関係にあるとき、
，
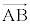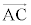は1次独立であると言います。
ベクトルの成分表示 原点Oを始点とするベクトルを位置ベクトルと言います。座標平面上で点Pの位置ベクトル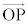
を考えるとき、点Pの座標をベクトルのように扱うことができます。これを
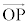の成分表示と言います。
内積 内積は2つのベクトルの大きさと位置関係により決まる量です。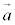
，
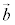のなす角をθ として、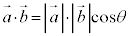
三角形の面積の公式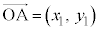 
，
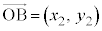とするとき、△OABの面積は、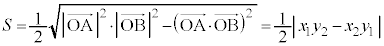
ベクトルの内分・外分 線分ABをm：nに内分する点Pの位置ベクトルは、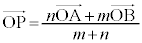
，m：nに外分する点Qの位置ベクトルは、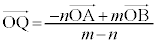
直線のベクトル方程式 2点A，Bを通る直線上の点Pを規定する式、つまり、点Aを通り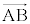
に平行な直線のベクトル方程式は、tを実数として、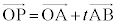
平面ベクトルの応用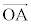 
，
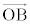が1次独立で、s，tを実数として、
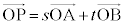という関係があるとき、
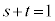ならPは直線AB上の点
共線条件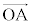 
，
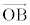が1次独立で、s，tを実数として、
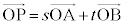という関係があるとき、Pが直線AB上の点なら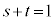
円のベクトル方程式 C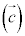
を中心とし、半径rの円周上の点P
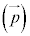が満たす、円のベクトル方程式は、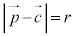
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。