���������@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�O�p�`OAB������Ƃ�(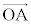 �C
�C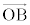 ��1���Ɨ��ł���Ƃ�)�A
��1���Ɨ��ł���Ƃ�)�A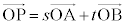 �Ŏw�肳���_P������OA��ɑ��݂�������́A
�Ŏw�肳���_P������OA��ɑ��݂�������́A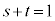
���̏��������̃E�F�u�T�C�g�ł́A���������ƌ������Ƃɂ��܂��B
�_P�Ɠ_A����v����Ƃ��ɂ́A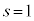 �C
�C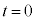 �̂Ƃ��A
�̂Ƃ��A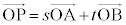 �ƂȂ�܂����A
�ƂȂ�܂����A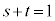 ����������Ă��܂��B
����������Ă��܂��B
�_P�Ɠ_B����v����Ƃ��ɂ́A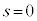 �C
�C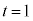 �̂Ƃ��A
�̂Ƃ��A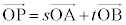 �ƂȂ�܂����A
�ƂȂ�܂����A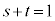 ����������Ă��܂��B
����������Ă��܂��B
�_P������AB��m�Fn�ɓ�������_�ł���Ƃ��A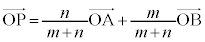 (�x�N�g���̓����E�O�����Q��)�C
(�x�N�g���̓����E�O�����Q��)�C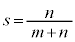 �C
�C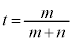 �Ƃ��āA
�Ƃ��āA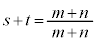 ���A
���A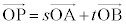 �ƂȂ�܂����A
�ƂȂ�܂����A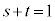 ����������Ă��܂��B
����������Ă��܂��B
�_P������AB��m�Fn�ɊO������_�ł���Ƃ��A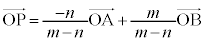 (�x�N�g���̓����E�O�����Q��)�C
(�x�N�g���̓����E�O�����Q��)�C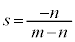 �C
�C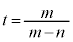 �Ƃ��āA
�Ƃ��āA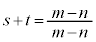 ���A
���A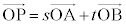 �ƂȂ�܂����A
�ƂȂ�܂����A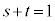 ����������Ă��܂��B
����������Ă��܂��B
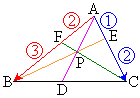 ��D�O�p�`ABC�̕�AB��2�F3�ɓ�������_��F�C��AC��1�F2�ɓ�������_��E�C����BE�Ɛ���CF�̌�_��P�Ƃ��A����AP�ƕ�BC�Ƃ̌�_��D�Ƃ���B
��D�O�p�`ABC�̕�AB��2�F3�ɓ�������_��F�C��AC��1�F2�ɓ�������_��E�C����BE�Ɛ���CF�̌�_��P�Ƃ��A����AP�ƕ�BC�Ƃ̌�_��D�Ƃ���B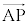 ��
��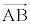 �C
�C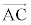 ��p���ĕ\���ABD�FDC�����߂�B
��p���ĕ\���ABD�FDC�����߂�B
[��1]�@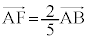 �@����@�C
�@����@�C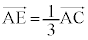 �@����A�@�ł��B
�@����A�@�ł��B
B�CP�CE�͈꒼����̓_�Ȃ̂ŁA�����������A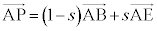 �@����B�@(�����������A
�@����B�@(�����������A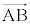 ��
��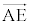 �̌W���𑫂���1�ɂȂ�܂��B
�̌W���𑫂���1�ɂȂ�܂��B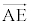 ��
��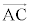 ���g���ĕ\�����x�N�g���Ȃ̂ŁA
���g���ĕ\�����x�N�g���Ȃ̂ŁA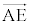 �̌W���̕����ȒP�Ȍ`�ɂ���悤��s�Ƃ��āA
�̌W���̕����ȒP�Ȍ`�ɂ���悤��s�Ƃ��āA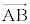 �̌W����
�̌W����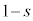 �Ƃ��Ă��܂�)
�Ƃ��Ă��܂�)
C�CP�CF�͈꒼����̓_�Ȃ̂ŁA�����������A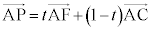 �@����C
�@����C
�B�ɇA�������āA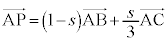 �@����D
�@����D
�C�ɇ@�������āA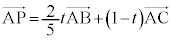 �@����E
�@����E
�D�C�E�̌W�����r���āA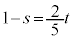 �C
�C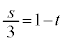
�A�����ĉ����ƁA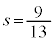 �C
�C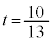
�D���A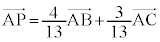 �@����F
�@����F
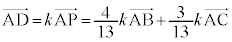 �@����G
�@����G
D�CB�CC���꒼����ɂ�������́A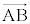 ��
��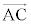 �̌W���̘a��1�ƂȂ邱�ƂŁA
�̌W���̘a��1�ƂȂ邱�ƂŁA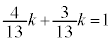
�� 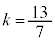
�G���A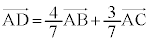
����́AD������BC��3�F4�ɓ�������_�ł��邱�Ƃ������B����āABD�FDC �� 3�F4 ......[��]
[��2]�@���l���E�X�̒藝���A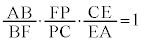
�� 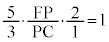
�� FP�FPC �� 3�F10
�� 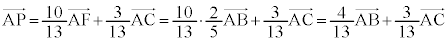
�`�F�o�̒藝���A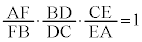
�� 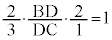
�� BD�FDC �� 3�F4 ......[��]
���D���܂�ɓT�^���Ȃ̂ňӊO�Əo�肳��܂��A��w�����ł́A��2�œ��Ă������܂��傤�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B