円のベクトル方程式
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
中心の位置ベクトルが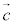 ,半径rの円周上の点の位置ベクトル
,半径rの円周上の点の位置ベクトル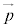 は、
は、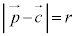 を満たします。
を満たします。
これが、ベクトルを用いた円の方程式です。
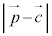 は円周上の点と円の中心との距離を表すので、それが半径rで一定となれば、
は円周上の点と円の中心との距離を表すので、それが半径rで一定となれば、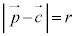 ・・・① が円を表すのは明らかでしょう。
・・・① が円を表すのは明らかでしょう。
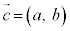 ,
,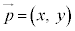 として、①式で、成分表示を考えてみます。
として、①式で、成分表示を考えてみます。
①式両辺を2乗して、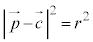
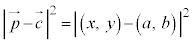
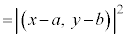
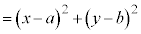 より、
より、
①は、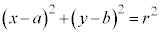 となります。
となります。
これは座標平面上で考えたときの円の方程式です。
①式とは違った形をしていますが、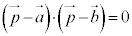 も円を表します。
も円を表します。
左辺を展開して、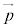 について平方完成と同様の操作を行うと、
について平方完成と同様の操作を行うと、
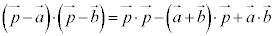
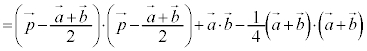
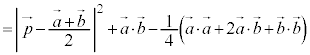
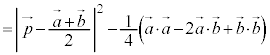
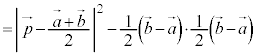
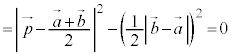
∴ 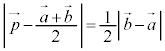 ・・・②
・・・②
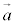 ,
,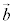 を点A,点Bの位置ベクトルだとして、
を点A,点Bの位置ベクトルだとして、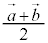 は、2点A,Bの中点の位置ベクトルです。
は、2点A,Bの中点の位置ベクトルです。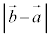 は2点AB間の距離です。
は2点AB間の距離です。
従って、②式は、A,Bの中点を中心として、AB間の距離の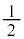 を半径とする円ということになります。これは、線分ABを直径とする円です。
を半径とする円ということになります。これは、線分ABを直径とする円です。
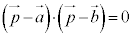 は、
は、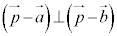 ,つまり、円周上の点Pについて、
,つまり、円周上の点Pについて、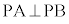 であることを言っている式です。
であることを言っている式です。
点H,C,Pの位置ベクトルを、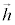 ,
,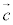 ,
,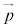 として、
として、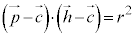 ・・・③ は、Cを中心とする半径rの円周上の点Hにおける接線を表します。
・・・③ は、Cを中心とする半径rの円周上の点Hにおける接線を表します。
Hが円周上の点であることから、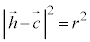 より、
より、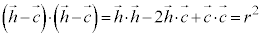
よって、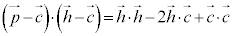
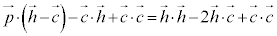
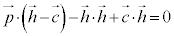
∴ 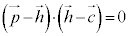
これは、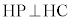 ,つまり、接線上の点Pと接点Hを結ぶ直線と半径HCが垂直であることを意味しています。
,つまり、接線上の点Pと接点Hを結ぶ直線と半径HCが垂直であることを意味しています。
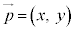 ,
,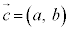 ,
,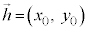 として③を成分表示してみます。
として③を成分表示してみます。
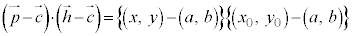
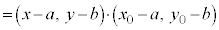
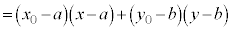
よって、C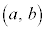 を中心とする半径rの円:
を中心とする半径rの円: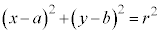 のH
のH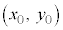 における接線の方程式は、
における接線の方程式は、
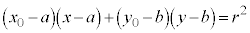
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
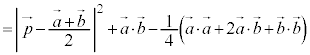
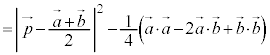
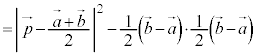
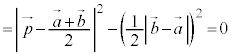
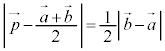 ・・・②
・・・②