2次曲線に関する問題(その5)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
離心率e (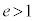 ),焦点と準線の距離がh,焦点を極とする双曲線の極方程式は、
),焦点と準線の距離がh,焦点を極とする双曲線の極方程式は、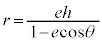 です。
です。
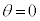 とすると、
とすると、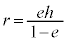 (
(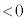 )となりますが、このとき、曲線上の点Cは、極(焦点)から、始線と反対側に距離
)となりますが、このとき、曲線上の点Cは、極(焦点)から、始線と反対側に距離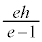 のところに来ます。
のところに来ます。
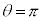 とすると、
とすると、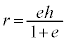 となりますが、このとき、曲線上の点Dは、極から、始線と反対側に距離
となりますが、このとき、曲線上の点Dは、極から、始線と反対側に距離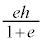 のところに来ます。
のところに来ます。
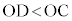 なので、左から、C,D,Oの順に一直線上に並びます。
なので、左から、C,D,Oの順に一直線上に並びます。
CDの中点M(双曲線の中心)は、DからC側に、距離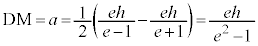 のところにあります。
のところにあります。
Mと焦点との距離を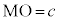 とすると、
とすると、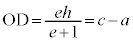 より、
より、
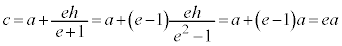
 Mと準線との距離は、
Mと準線との距離は、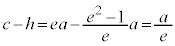 (
( )
)
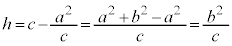
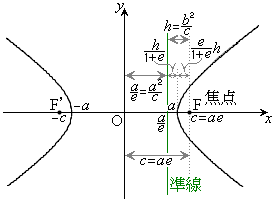
以上では、Oを双曲線の焦点としていましたが、改めてOをxy座標系の原点(双曲線の中心)にとると、双曲線: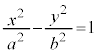 は、右図のようになっています。
は、右図のようになっています。
2次曲線に関する問題(その4)で、楕円の問題を極座標で考える例を示しました。
ここでは、さらに、一般の2次曲線に関する問題について、極座標で考える例を取り上げます。
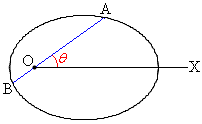 例1.極Oを焦点とする、極方程式:
例1.極Oを焦点とする、極方程式: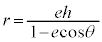 (離心率:
(離心率: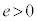 ,焦点Oと準線との距離:
,焦点Oと準線との距離: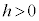 )で与えられる2次曲線と、焦点Oを通る直線との交点をA,Bとするとき、
)で与えられる2次曲線と、焦点Oを通る直線との交点をA,Bとするとき、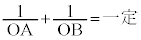 を証明する。
を証明する。
[証明] Aの偏角をθ とすると、Bの偏角は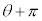 で与えられます。
で与えられます。
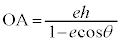 ,
,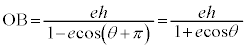
よって、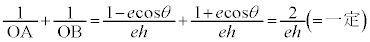 (証明終)
(証明終)
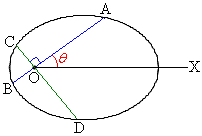 例2.極Oを焦点とする、極方程式:
例2.極Oを焦点とする、極方程式: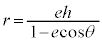 で与えられる2次曲線と、焦点Oを通る直線との交点をA,B,この直線と焦点Oで直交する直線との交点をC,Dとするとき、
で与えられる2次曲線と、焦点Oを通る直線との交点をA,B,この直線と焦点Oで直交する直線との交点をC,Dとするとき、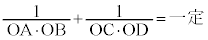 を証明する。
を証明する。
[証明] 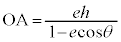 ,
,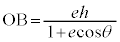
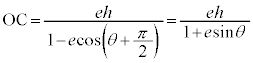 ,
,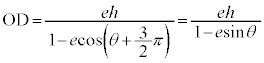
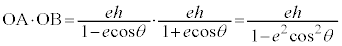
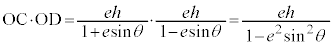
よって、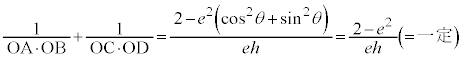 (証明終)
(証明終)
極方程式: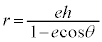 によって、楕円(
によって、楕円(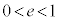 )と双曲線(
)と双曲線(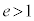 )と放物線(
)と放物線(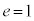 )を、焦点を極とする極座標でまとめて扱うことができますが、標準形で表された楕円と双曲線については、中心(xy座標系の原点O)を極とする極方程式も考えられます。
)を、焦点を極とする極座標でまとめて扱うことができますが、標準形で表された楕円と双曲線については、中心(xy座標系の原点O)を極とする極方程式も考えられます。
楕円: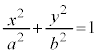 (
(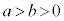 )では、
)では、
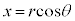 ,
,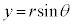 を代入すると、
を代入すると、
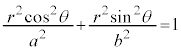
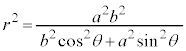
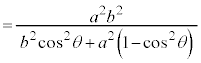
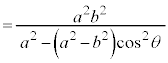
分母、分子を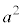 で割り、
で割り、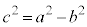 (cは焦点の座標),
(cは焦点の座標),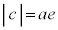 (eは離心率、2次曲線に関する問題(その4)を参照)を用いると、
(eは離心率、2次曲線に関する問題(その4)を参照)を用いると、
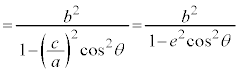
双曲線: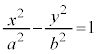 では、
では、
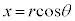 ,
,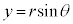 を代入すると、
を代入すると、
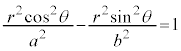
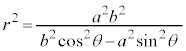
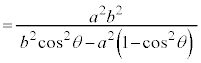
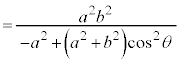
分母、分子を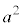 で割り、
で割り、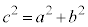 (cは焦点の座標),
(cは焦点の座標),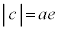 (eは離心率、このページの上記を参照)を用いると、
(eは離心率、このページの上記を参照)を用いると、
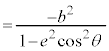
中心を極とする極座標における極方程式は、
楕円では、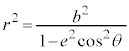
双曲線では、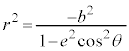
となります。
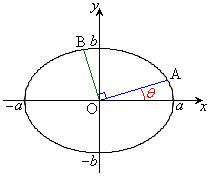 例3.中心をOとする、楕円:
例3.中心をOとする、楕円: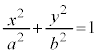 (
(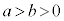 )または、双曲線:
)または、双曲線: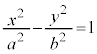 (
(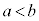 )上に2点A,Bをとり、
)上に2点A,Bをとり、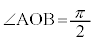 とすると、
とすると、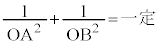 となることを証明する。
となることを証明する。
[証明] 楕円の場合、中心を極とする楕円の極方程式: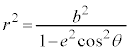 を用いると、
を用いると、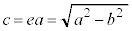 より、
より、
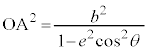 ,
,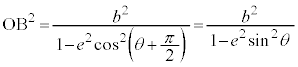
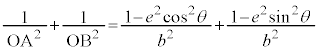
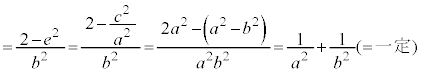
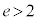 となる双曲線の場合、同様にして、
となる双曲線の場合、同様にして、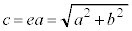 より、
より、
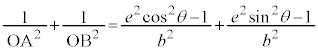
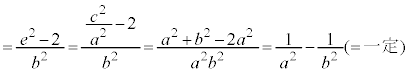 (証明終)
(証明終)
注.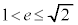 となる双曲線の場合、
となる双曲線の場合、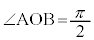 となるような2点A,Bを双曲線上に取ることができません。
となるような2点A,Bを双曲線上に取ることができません。
 例4.中心をOとする、楕円:
例4.中心をOとする、楕円: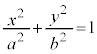 (
(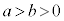 )上に3点A,B,Cをとり、
)上に3点A,B,Cをとり、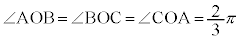 とすると、
とすると、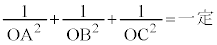 となることを証明する。
となることを証明する。
[証明] 中心を極とする楕円の極方程式: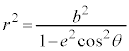 を用いると、
を用いると、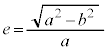 より、
より、
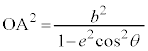
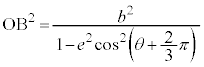
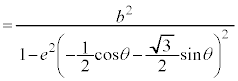
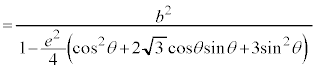
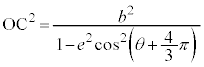
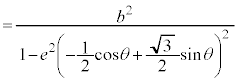
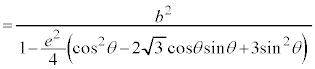
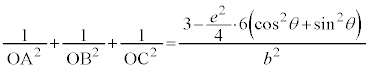
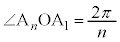 (証明終)
(証明終)
注.楕円上にn個の点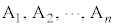 を、
を、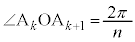 (
(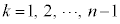 )のようにとるとき、
)のようにとるとき、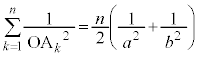 が言えます。
が言えます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  )
)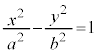 は、右図のようになっています。
は、右図のようになっています。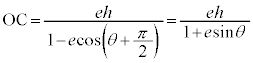 ,
,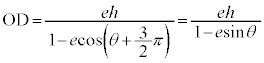
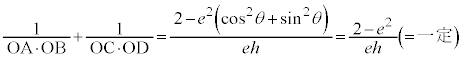 (証明終)
(証明終)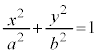 (
(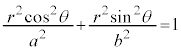
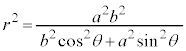
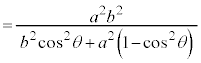
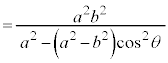
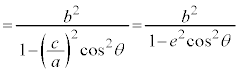
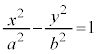 では、
では、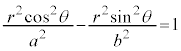
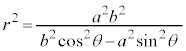
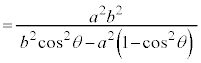
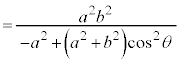
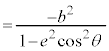
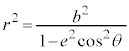
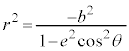
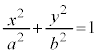 (
(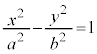 (
(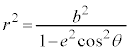 を用いると、
を用いると、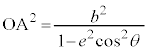 ,
,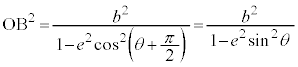
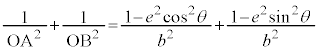
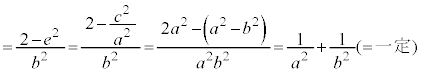
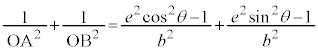
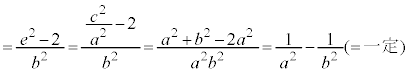 (証明終)
(証明終)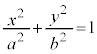 (
(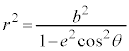 を用いると、
を用いると、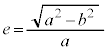 より、
より、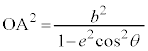
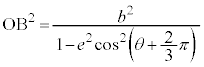
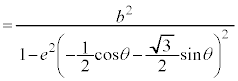
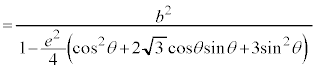
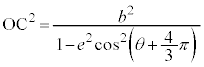
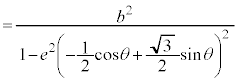
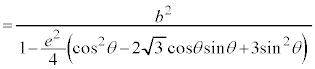
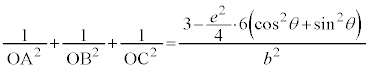
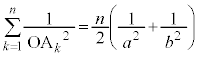 が言えます。
が言えます。