2���Ȑ��Ɋւ�����(����4)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�ȉ~�̖����ɍ��W���g���čl���Ă݂܂��B
�ȉ��̗���Axy���W�n�ŕ��ʂɂ���Ă݂܂��B
��1�D�ȉ~�F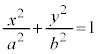 (
(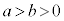 )�̏œ_
)�̏œ_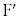
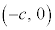 ��ʂ钼��l�Ƒȉ~�Ƃ̌�_��A�CB�Ƃ��A������̏œ_��F
��ʂ钼��l�Ƒȉ~�Ƃ̌�_��A�CB�Ƃ��A������̏œ_��F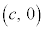 �Ƃ���Ƃ��A�O�p�`FAB�̖ʐς̍ő�l�����߂�B�A���A
�Ƃ���Ƃ��A�O�p�`FAB�̖ʐς̍ő�l�����߂�B�A���A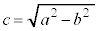
 [��]�@�ȉ~�̕������̕�����āA
[��]�@�ȉ~�̕������̕�����āA
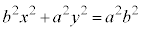 �@����@
�@����@
�œ_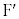
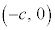 ��ʂ钼��l�́Ax���ɐ����ɂȂ�Ƃ��������āA
��ʂ钼��l�́Ax���ɐ����ɂȂ�Ƃ��������āA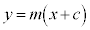 �@����A�@(�ȉ~��x���Ɋւ��đΏ̂Ȃ̂ŁA
�@����A�@(�ȉ~��x���Ɋւ��đΏ̂Ȃ̂ŁA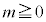 �Ƃ��ď\���ł�)
�Ƃ��ď\���ł�)
������@�ɑ�����āA
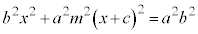
��������ƁA
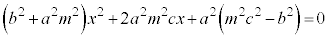 �@����B
�@����B
����AB�̒���d�́A�B��2����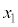 �C
�C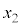 �Ƃ��āA
�Ƃ��āA
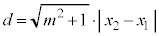
�A���A����l��x���ɐ����ɂȂ�Ƃ��ɂ́A�ȉ~�̕������ŁA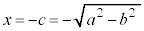 �Ƃ��āA
�Ƃ��āA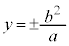
���̂Ƃ��́A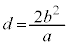 �@����C
�@����C
�ƍl���܂��B
�B��2���̍��́A�B�̔��ʎ���D�Ƃ��āA
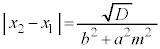 �@(2���������̈�ʘ_���Q�ƁA2���������F
�@(2���������̈�ʘ_���Q�ƁA2���������F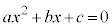 �̔��ʎ���
�̔��ʎ���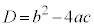 �Ƃ��āA2���̍��́A
�Ƃ��āA2���̍��́A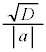 )
)
�����ŁA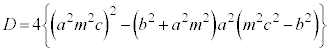
�@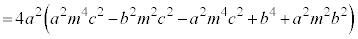
�@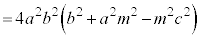
�@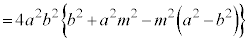
�@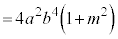
�� 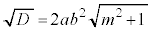
����āA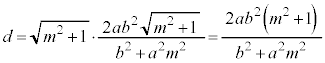
�C�́A������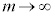 �Ƃ����Ƃ��̋Ɍ��ɂȂ��Ă��܂��B
�Ƃ����Ƃ��̋Ɍ��ɂȂ��Ă��܂��B
���āAF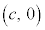 �ƒ����A�Ƃ̋���h�́A
�ƒ����A�Ƃ̋���h�́A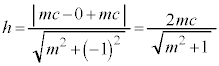
�O�p�`FAB�̖ʐ�S�́A
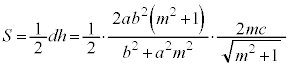
�@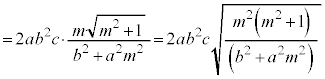
��������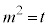 (
(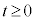 )�Ƃ����āA
)�Ƃ����āA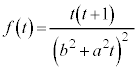
���̓����́A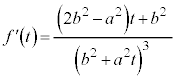
�E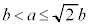 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A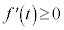 �Ȃ̂ŁA
�Ȃ̂ŁA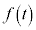 �͒P�������ł��B����āA
�͒P�������ł��B����āA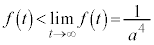
�]���āAS�̍ő�l�́A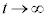 �Ƃ����Ƃ��A�܂�A�����A��x���ɐ����ȂƂ��A
�Ƃ����Ƃ��A�܂�A�����A��x���ɐ����ȂƂ��A
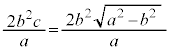 ......[��]
......[��]
�E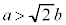 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A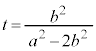 �ɂ����āA
�ɂ����āA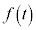 �͋ɑ�ƂȂ�AS�̍ő�l�́A
�͋ɑ�ƂȂ�AS�̍ő�l�́A
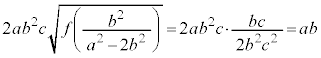 ......[��]
......[��]
xy���W�n�ōl���Ă����Ƃ������܂����A���������A�ɍ��W���g���čl���Ă݂܂��B
��2�D�ɕ������F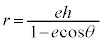 (
(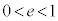 �C
�C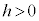 )�ŗ^������ȉ~(��O�ɏœ_������A���S����e�C�����͎n���ɐ����ŏœ_�Ƃ̋�����h)�Ƃ��̏œ_��ʂ钼���Ƃ̌�_��A�CB�Ƃ��A�ɂłȂ����̏œ_��F�Ƃ���Ƃ��A�O�p�`FAB�̖ʐς̍ő�l�����߂�B
)�ŗ^������ȉ~(��O�ɏœ_������A���S����e�C�����͎n���ɐ����ŏœ_�Ƃ̋�����h)�Ƃ��̏œ_��ʂ钼���Ƃ̌�_��A�CB�Ƃ��A�ɂłȂ����̏œ_��F�Ƃ���Ƃ��A�O�p�`FAB�̖ʐς̍ő�l�����߂�B
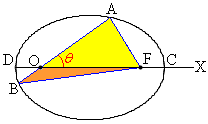 [��]�@A�CB�͑ȉ~��̓_�Ȃ̂ŁA�ȉ~�̕����������܂��BA�̕Ίp(OA��x���̂Ȃ��p)��θ (
[��]�@A�CB�͑ȉ~��̓_�Ȃ̂ŁA�ȉ~�̕����������܂��BA�̕Ίp(OA��x���̂Ȃ��p)��θ (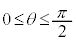 �Ƃ��čl����Ώ\���ł�)�Ƃ���ƁAB�̕Ίp��
�Ƃ��čl����Ώ\���ł�)�Ƃ���ƁAB�̕Ίp��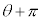 �ł��B
�ł��B
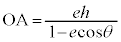 �C
�C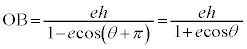
�ȉ~�Ǝn���Ƃ̌�_��C�C�n���̋ɑ��ւ̉������Ƃ̌�_��D�Ƃ���ƁA
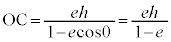 �C
�C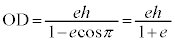
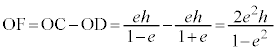
�O�p�`FAB�̖ʐ�S�́A
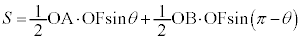
�@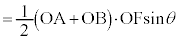
�@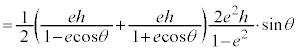
�@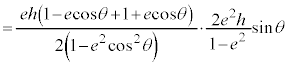
�@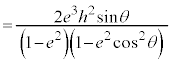 �@����@
�@����@
�@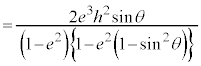
�@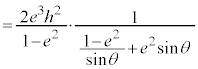 �@(
�@(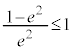 �C�܂�A
�C�܂�A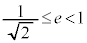 �̂Ƃ��ɂ́A�������ρA���敽�ς̊W���g���܂��B�s�����̏ؖ����Q��)
�̂Ƃ��ɂ́A�������ρA���敽�ς̊W���g���܂��B�s�����̏ؖ����Q��)
�@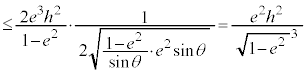
��L�̕s�����ŁA��������������̂́A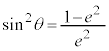 �C�܂�A
�C�܂�A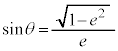 �̂Ƃ��ł����A
�̂Ƃ��ł����A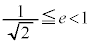 �̂Ƃ��ɂ́A�������θ �����݂���̂ŁAS�̍ő�l�́A
�̂Ƃ��ɂ́A�������θ �����݂���̂ŁAS�̍ő�l�́A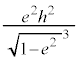 ......[��]
......[��]
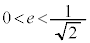 �̂Ƃ��́A�@�ɂ����āA
�̂Ƃ��́A�@�ɂ����āA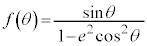 �Ƃ����ƁA
�Ƃ����ƁA
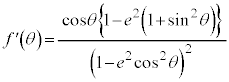
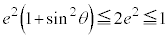 ���A
���A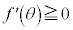 (
(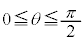 )
)
����āA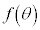 �́A
�́A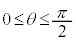 �ɂ����āA�P�������ł��B
�ɂ����āA�P�������ł��B
�� 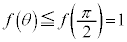
���̂Ƃ��ɂ́A�@���AS�̍ő�l�́A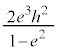 ......[��]
......[��]
��2�̒��ŁA���łɁA�ȉ~�̒����̒��������߂�ƁA
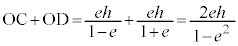
������A�ȉ~�F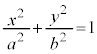 (
(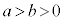 )�ɂ����āA
)�ɂ����āA
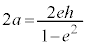 �Ƃ��āA
�Ƃ��āA
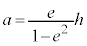
�œ_��x���W��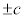 (
(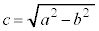 )�Ƃ��āA
)�Ƃ��āA
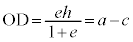 ���A
���A
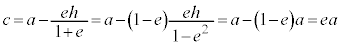
 �����Ƒȉ~�̒��S�Ƃ̋����́A
�����Ƒȉ~�̒��S�Ƃ̋����́A
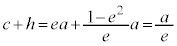 (
(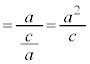 )
)
�܂��A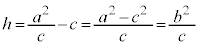
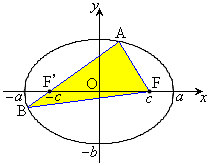
��2��O�́A��(�ȉ~�̏œ_)�ł������A���߂āAxy���W�n�̌��_��O (�ȉ~�̒��S)�ɂƂ�ƁA�ȉ~�F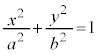 (
(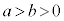 )�́A�E�}�̂悤�ɂȂ��Ă��܂��B
)�́A�E�}�̂悤�ɂȂ��Ă��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 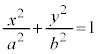 (
(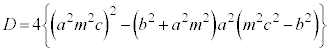
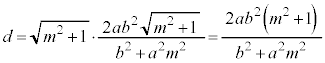
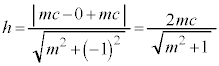
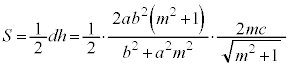
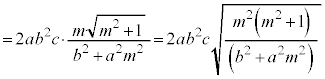
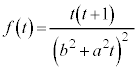
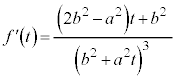
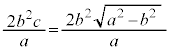 ......[��]
......[��]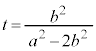 �ɂ����āA
�ɂ����āA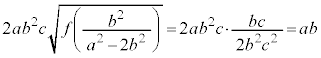 ......[��]
......[��]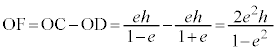
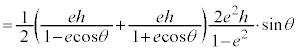
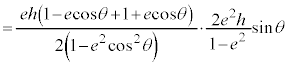
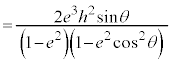 �@����@
�@����@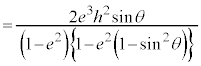
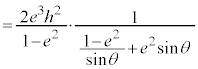 �@(
�@(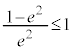 �C�܂�A
�C�܂�A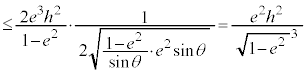
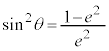 �C�܂�A
�C�܂�A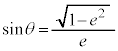 �̂Ƃ��ł����A
�̂Ƃ��ł����A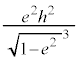 ......[��]
......[��]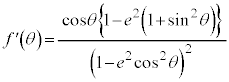
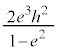 ......[��]
......[��]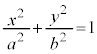 (
(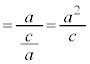 )
)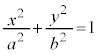 (
(