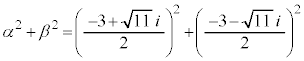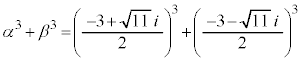2���������̉��ƌW���̊W�̉��p�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
2���������F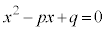 ��2��(�������ł����Ă��悢)��α�Cβ �Ƃ��āA
��2��(�������ł����Ă��悢)��α�Cβ �Ƃ��āA
2���������̉��ƌW���̊W�F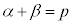 �C
�C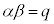
2���������F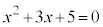 ��2����α�Cβ �Ƃ��āA
��2����α�Cβ �Ƃ��āA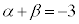 �C
�C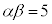 �ł��B
�ł��B
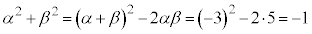
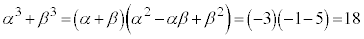
�ȂǂƂ��āA���ƌW���̊W�𗘗p���邱�Ƃɂ��Aα�Cβ �Ɋւ���Ώ̎��̒l���ȕւɌv�Z���Ă������Ƃ��ł��܂��B
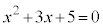 ��2���́A
��2���́A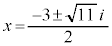 �ł����A
�ł����A
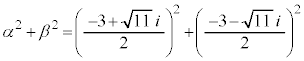
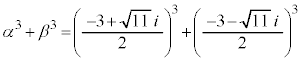
�Ȃǂƌv�Z����Ƒ�ςȂ��ƂɂȂ�܂��B
���f���̐����F�g�����̋��f���͂��Ƃ̎����h(����a�ɂ��āA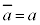 )�Ƃ����������g���ƁA
)�Ƃ����������g���ƁA
�����W����2���������F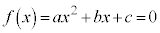 (a�Cb�Cc�͎���)
(a�Cb�Cc�͎���)
���������Ƃ��ɁA����2���������̉���1��α�Ƃ��āA
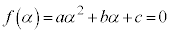 ���A
���A
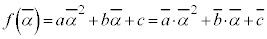
�@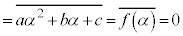
����āA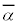 ��2���������F
��2���������F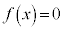 �̉��ł��B
�̉��ł��B
�܂�A�����W����2���������ɂ��āA1�̋��������ł���A���̋��f�������ɂȂ�܂��B
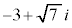 �����Ɏ������W���̕����������A�Ƃ�����肪����܂��B
�����Ɏ������W���̕����������A�Ƃ�����肪����܂��B
�����W���̕������ł���A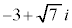 �̋��f��
�̋��f��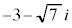 ���܂����ɂȂ�܂��B
���܂����ɂȂ�܂��B
2���̘a�F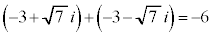
2���̐ρF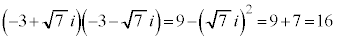
���A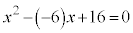 �C�܂�A
�C�܂�A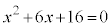 �����߂�2���������Ƃ������ƂɂȂ�܂��B
�����߂�2���������Ƃ������ƂɂȂ�܂��B
(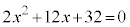 �Ȃǂł��悢)
�Ȃǂł��悢)
2���������F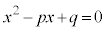 �̔��ʎ��F
�̔��ʎ��F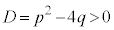 �ł���Ƃ��A2��������α�Cβ ���Ƃ��āA
�ł���Ƃ��A2��������α�Cβ ���Ƃ��āA
1) 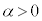 ����
����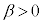 ��
�� 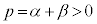 ����
����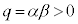
2) 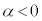 ����
����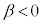 ��
�� 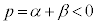 ����
����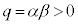
3) α�Cβ ���ٕ��� �� 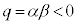
�����藧���܂��B����𗘗p���ĉ�����肪����܂��B
��D2���������F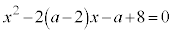 ��2���������A
��2���������A
(1) �Ƃ��ɐ����@(2) �Ƃ��ɕ����@(3) �ٕ���
�ƂȂ�悤�ɁA�萔a�͈̔͂��߂�B
[��]�@2����������2�������������߂ɁA
���ʎ��F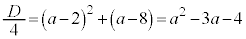
�@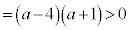
�� 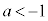 �܂���
�܂��� 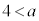 ����@
����@
�ȉ��A���̏������ōl���܂��B
(1) 2�����Ƃ��ɐ��� �� 2���̘a�F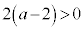 ���� 2���̐ρF
���� 2���̐ρF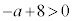
�� 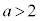 ����
���� 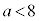
�@�ƍ��킹�āA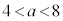 ......[��]
......[��]
(2) 2�����Ƃ��ɕ��� �� 2���̘a�F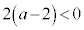 ���� 2���̐ρF
���� 2���̐ρF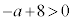
�� 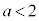 ����
���� 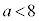
�@�ƍ��킹�āA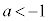 ......[��]
......[��]
(3) 2�����ٕ��� �� 2���̐ρF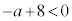
�@�ƍ��킹�āA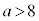 ......[��]
......[��]
���D���̃^�C�v�̖��ɂ��ẮA2���������̉��̔z�u���Q�ƁB
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B