���H�吔�w'06�N�O��[4]
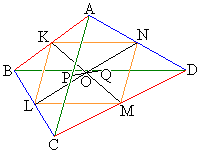
��ԓ��̎l�ʑ�ABCD���l����B��AB�CBC�CCD�CDA�̒��_���A���ꂼ��K�CL�CM�CN�Ƃ���B
(1) 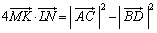 �������B������
�������B������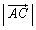 �̓x�N�g��
�̓x�N�g��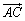 �̒�����\���B
�̒�����\���B (2) �l�ʑ�ABCD�̂��ׂĂ̖ʂ��݂��ɍ����ł���Ƃ���B���̂Ƃ�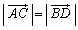 �C
�C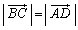 �C
�C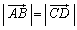 �������B
�������B (3) ��AC�̒��_��P�Ƃ��A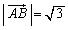 �C
�C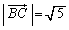 �C
�C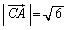 �Ƃ���B(2)�̉���̂��ƂŁA�l�ʑ�PKLN�̑̐ς����߂�B
�Ƃ���B(2)�̉���̂��ƂŁA�l�ʑ�PKLN�̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ŋ߁A����A����Ȃǂŏo�肳��Ă��铙�ʎl�ʑ̂Ɋւ�����ŁA������ABCD-EFGH�̊e�ʂ̑Ίp���ƒ��_�Ƃłł���l�ʑ̂̂����AABDE�CBCDG�CEFGB�CEGHD��4����菜���ƁA���ʎl�ʑ̂��ł���A�Ƃ����m�����g�������ɂł���̂ł����A�����ł́A�O��m����z�肵�Ȃ��ł���Ă݂܂��B�Ȃ��A��ԃx�N�g�����Q�Ƃ��Ă��������B
 (1)
(1) 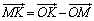
�� 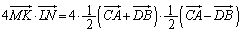
(2) �e�ʂ����O�p�`�A�ӎO�p�`�ł��邱�Ƃ͑z�肳��Ă��Ȃ��̂ŁA�e�ʂƂ��ӂ̒������قȂ���̂Ƃ��āA�O�p�`ABC�ɂ����āA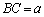 �C
�C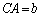 �C
�C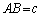 (a�Cb�Cc�݂͌��ɈقȂ鐳��)�Ƃ��܂��B���̏ꍇ�ł��A��ӂ͐������Ȃ���Ȃ�܂���B
(a�Cb�Cc�݂͌��ɈقȂ鐳��)�Ƃ��܂��B���̏ꍇ�ł��A��ӂ͐������Ȃ���Ȃ�܂���B 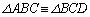 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA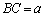 �Ȃ̂ŁA
�Ȃ̂ŁA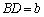 �C
�C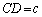 �@����@ �ƂȂ邩�A�܂��́A
�@����@ �ƂȂ邩�A�܂��́A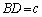 �C
�C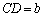 �@����A �ƂȂ邩�̂����ꂩ2�ʂ�̉\����������܂���B
�@����A �ƂȂ邩�̂����ꂩ2�ʂ�̉\����������܂���B
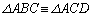 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA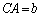 �Ȃ̂ŁA
�Ȃ̂ŁA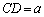 �C
�C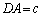 �@����B �ƂȂ邩�A�܂��́A
�@����B �ƂȂ邩�A�܂��́A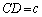 �C
�C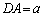 �@����C �ƂȂ邩�̂����ꂩ2�ʂ�̉\����������܂���B
�@����C �ƂȂ邩�̂����ꂩ2�ʂ�̉\����������܂���B
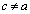 ���A�@���B�͂��蓾�܂���B
���A�@���B�͂��蓾�܂���B
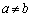 ���A�A���B�͂��蓾�܂���B
���A�A���B�͂��蓾�܂���B
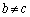 ���A�A���C�͂��蓾�܂���B
���A�A���C�͂��蓾�܂���B
����āA�g�@���C�h�̏ꍇ�ɍi���܂����A���̂Ƃ��A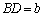 �C
�C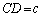 �C
�C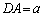 �ƂȂ�܂��B
�ƂȂ�܂��B
���̂Ƃ��A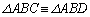 ���A�l�ʑ�ABCD�̂��ׂĂ̖ʂ��݂��ɍ����ɂȂ�܂��B
���A�l�ʑ�ABCD�̂��ׂĂ̖ʂ��݂��ɍ����ɂȂ�܂��B
���̂Ƃ��A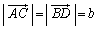 �C
�C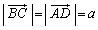 �C
�C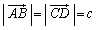
(3) (2)�̉���̂��ƂŁA(1)���A
����āA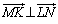 �ł��B
�ł��B ���l�ɁA
����āA KL // NM�C�܂��A
KL // NM�C�܂��A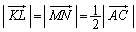 �@����D
�@����D
������A�l�p�`KLMN�́A���s�l�ӌ`�ł����A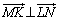 ���A���s�l�ӌ`�̑Ίp������������̂ŁA�l�p�`KLMN�͂Ђ��`�ł��BMK��LN�̌�_��O�Ƃ���ƁAO��MK�CLN�̒��_�ł���A�܂��A
���A���s�l�ӌ`�̑Ίp������������̂ŁA�l�p�`KLMN�͂Ђ��`�ł��BMK��LN�̌�_��O�Ƃ���ƁAO��MK�CLN�̒��_�ł���A�܂��A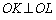
�S�����l�ɂ��āABD�̒��_��Q�Ƃ���ƁA�l�p�`PKQM�͂Ђ��`�ŁAMK�̒��_��O�Ȃ̂ŁAPQ�̒��_��O�ƂȂ�A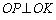 �C
�C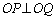 (MK��LN��PQ��1�_O�Ō݂��ɐ����Ɍ����܂�)�D�Ɠ��l�ɂ��āA
(MK��LN��PQ��1�_O�Ō݂��ɐ����Ɍ����܂�)�D�Ɠ��l�ɂ��āA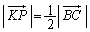 �C
�C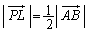
�O�����̒藝���A (�E�{�F�{�G)��2���A
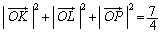 �@����H
�@����H�H�|�G���A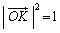
�H�|�F���A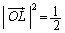
�H�|�E���A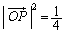
�l�ʑ�PKLN�̒�ӂ��O�p�`KLN�ƌ���ƁA���̖ʐς͎O�p�`OKL�̖ʐ�2���ŁA�l�ʑ̂̍�����OP����Ă��l�ʑ�PKLN�̑̐ς́A 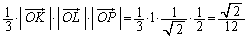 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B