東工大数学'07年前期[3]
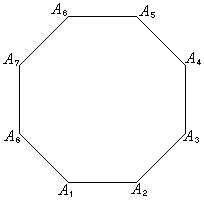 一辺の長さが1の正八角形
一辺の長さが1の正八角形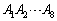 の周上を3点P,Q,Rが動くとする。
の周上を3点P,Q,Rが動くとする。
(1) 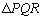 の面積の最大値を求めよ。
の面積の最大値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 最大値そのものはすぐわかるのですが、論証するのが難しい問題です。もちろん、解答のみの答案では正解でも零点でしょう。(1)も(2)も場合分けの方法を充分に考えてから取り組むことになります。
(1) 点Pを辺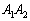 上に取り、
上に取り、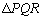 の面積をSとします。
の面積をSとします。 (i) 点Qを辺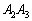 上に取ります。点Rを辺
上に取ります。点Rを辺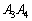 上、辺
上、辺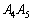 上、辺
上、辺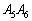 上、辺
上、辺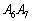 上、辺
上、辺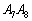 上、辺
上、辺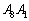 上で動かします。
上で動かします。 (ii) 点Qを辺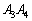 上に取ります。
上に取ります。
(a) 点Rを辺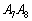 上に取ります。
上に取ります。 (b) 点Rを辺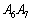 上に取ります。
上に取ります。
PQと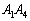 との距離をx (
との距離をx (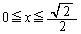 )として、
)として、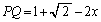 ,PQと
,PQと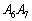 との距離は、
との距離は、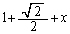 ,よって、
,よって、 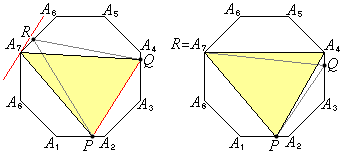 ・PQが
・PQが と平行でないとき、
と平行でないとき、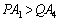 だとします(
だとします(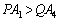 も同様です)。
も同様です)。
(2) 右図でPを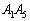 の左上側、Rを右下側として、一般性を失いません。
の左上側、Rを右下側として、一般性を失いません。 Pが辺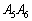 上の
上の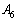 以外の点の場合、題意を満たすRを取ることができません。Rが辺
以外の点の場合、題意を満たすRを取ることができません。Rが辺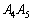 上の
上の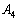 以外の点の場合、題意を満たすPを取ることができません。
以外の点の場合、題意を満たすPを取ることができません。 (i) Pが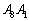 上(
上(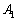 を除く)ならRは
を除く)ならRは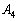 に来ます。また、Rが
に来ます。また、Rが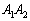 上(
上(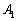 を除く)なら、Pは
を除く)なら、Pは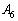 に来ます。
に来ます。 この場合のSの最大値は、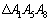 の面積に等しく、
の面積に等しく、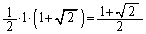
(ii) 右上図より、Pが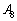 に来るとき、Rは
に来るとき、Rは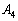 に来ます。また、Pが
に来ます。また、Pが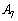 に来るとき、Rは
に来るとき、Rは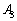 に来ます。
に来ます。 右下図より、
(a) Pが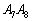 上に来るとき、Rは
上に来るとき、Rは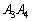 上に来ます。
上に来ます。 (b) Pが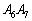 上に来るとき、Rは
上に来るとき、Rは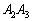 上に来ます。
上に来ます。 正八角形の対称性より、(a)と(b)には必ず対応する合同な三角形となる場合(右下図黄緑色の三角形)があり、どちらか一方を考えればよいので、(b)の場合で考えることにします。
これ以降、座標を考えてもできますが、距離を表すのに根号がついて計算が面倒になります。こういう場合には、どこかの角をθ とおいて、三角関数で考えるとうまくいくことがあります。
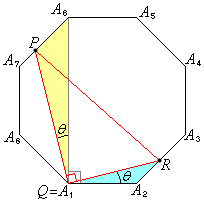 右図で、
右図で、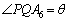 (
(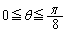 )とおくと、
)とおくと、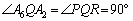 だから、
だから、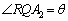 です。
です。
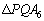 において、正弦定理より、
において、正弦定理より、 ∴ 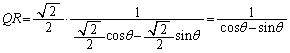 よって、
よって、 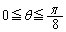 において、Sは単調増加で、
において、Sは単調増加で、
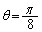 のとき、Sは最大値
のとき、Sは最大値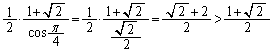 をとります。
をとります。以上より、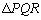 の面積の最大値は、
の面積の最大値は、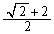 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東工大数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
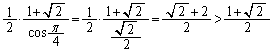 をとります。
をとります。