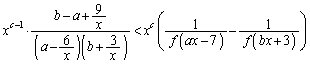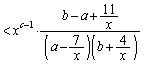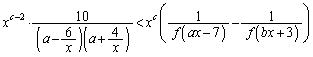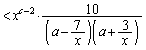���H�吔�w'08�N�O��[2]
����x�ɑ��Ax�ȏ�̍ŏ��̐�����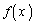 �Ƃ���Ba�Cb�𐳂̎����Ƃ���Ƃ��A�Ɍ�
�Ƃ���Ba�Cb�𐳂̎����Ƃ���Ƃ��A�Ɍ�
�@�@�@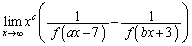
����������悤�Ȏ���c�̍ő�l�ƁA���̂Ƃ��̋Ɍ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����Ɍ����āA�債�����ƂȂ������ŁA����ς蓌�H�傾���̂��Ƃ͂���A�Ƃ������ł��B�ux�ȏ�̍ŏ��̐����v�̓K�E�X�L���Ɠ��l�̂��Ƃ��l����悢�͂��ł��Bn�𐮐��Cx�������Ƃ��āA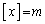 �̂Ƃ��A
�̂Ƃ��A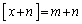 �Ȃ̂ŁA���̖��ł��A
�Ȃ̂ŁA���̖��ł��A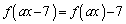 �Ȃǂƍl���邱�Ƃɂ��܂��B
�Ȃǂƍl���邱�Ƃɂ��܂��B
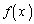 �́Ax�ȏ�̍ŏ��̐���������A
�́Ax�ȏ�̍ŏ��̐���������A
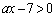 �ł���悤��x�ɑ��āA�@���A
�ł���悤��x�ɑ��āA�@���A
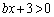 �ł���悤��x�ɑ��āA�A���A
�ł���悤��x�ɑ��āA�A���A
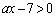 �C
�C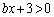 ���Ƃ��ɖ������悤��x�ɂ��āA
���Ƃ��ɖ������悤��x�ɂ��āA
���ӂƉE�ӂ�ό`���āA
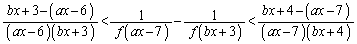
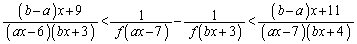 �@����B
�@����B(i) 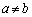 �̂Ƃ��A
�̂Ƃ��A �B�̊e�ӂ�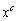 �������āA
�������āA ���߂�c�̍ő�l��1
(ii) 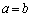 �̂Ƃ��Ac�̍ő�l��2���Ƃ������Ƃ͂����킩��܂����A
�̂Ƃ��Ac�̍ő�l��2���Ƃ������Ƃ͂����킩��܂����A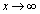 �̂Ƃ��A�B�̍��ӂƉE�ӂ������l�ɋ߂Â��Ă���Ȃ��̂ŁA�͂��݂������g���܂���B
�̂Ƃ��A�B�̍��ӂƉE�ӂ������l�ɋ߂Â��Ă���Ȃ��̂ŁA�͂��݂������g���܂���B �ŏ�����l���������Ƃɂ��܂��B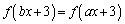 �ł��B����𐳂Ƃ���悤�ȏ\���ɑ傫��x�ɂ��āA
�ł��B����𐳂Ƃ���悤�ȏ\���ɑ傫��x�ɂ��āA 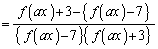
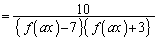 �@����C
�@����C����Ȃ�A�͂��݂������g���܂��B�@�ƇA��b��a�Ƃ����s��������A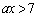 �ƂȂ�悤��x�ɂ��āA
�ƂȂ�悤��x�ɂ��āA ���̕s�����̊e�ӂ�10�{�������̂ƁA�C�Ƃ����킹�āA
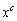 �������āA
�������āA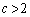 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A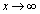 �̂Ƃ��A���ӁA�E�ӂ͂Ƃ��ɐ��̖�����ɔ��U���A
�̂Ƃ��A���ӁA�E�ӂ͂Ƃ��ɐ��̖�����ɔ��U���A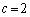 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A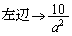 �C
�C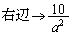
����āA�͂��݂����̌������A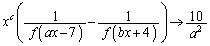
���߂�c�̍ő�l��2
(i) 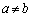 �̂Ƃ��Ac�̍ő�l�F1�C�Ɍ��l�F
�̂Ƃ��Ac�̍ő�l�F1�C�Ɍ��l�F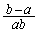
(ii) 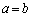 �̂Ƃ��Ac�̍ő�l�F2�C�Ɍ��l�F
�̂Ƃ��Ac�̍ő�l�F2�C�Ɍ��l�F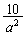 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B