東工大数学'09年後期[1]
aが与えられた実数のとき、xyz空間の点C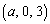
から出た光が球
でさえぎられてできるxy平面上の影をSとする。点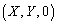
がSに含まれる条件を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 点光源による円の影が楕円になるという問題です。
Sの外周となる閉曲線をFとすると、Sは、曲線F及び曲線Fの内部、になります。
点B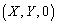
が曲線F上の点であるとき、BとCを結ぶ直線は、球の接線になっています。このとき、球の中心A
とCを結ぶ直線と、直線BCのなす角θ は一定です(Cを通る球の接線群と接点の集合の円とでCを頂点とする円錐を作ります)。ここに着眼します。
直線BCと球との接点をDとすると、
であり、三角形ADCは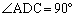
となる直角三角形なので、
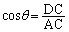です。
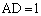より、
よって、
∴ 
両辺を2乗して、
∴ 
よって、曲線Fは楕円(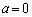
の場合の円も含む)であり、Sは楕円Fおよび楕円Fの内部、ということになります。点
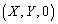がSに含まれる条件は、
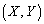が楕円
の周上または内部の点であること ......[答] です。
注．「大学への数学」'09年5月号に、直線BCのベクトル方程式と球の方程式を連立する解法が紹介されています。こちらもぜひ、参照してください。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
