���H�吔�w'09�N�O��[3]
N�𐳂̐����Ƃ���B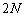 �ȉ��̐��̐���m�Cn����Ȃ�g
�ȉ��̐��̐���m�Cn����Ȃ�g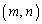 �ŁA������
�ŁA������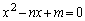 ��N�ȏ�̎����������悤�Ȃ��͉̂��g���邩�B
��N�ȏ�̎����������悤�Ȃ��͉̂��g���邩�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@150����4��Ȃ�A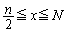 �͈̔͂Ɏ����������Ƃ��̊i�q�_�̐��𐔂���A�Ƃ������炢�łȂ��ƁA���H��̖��Ƃ��Ă͕�����Ȃ��C�����܂��B
�͈̔͂Ɏ����������Ƃ��̊i�q�_�̐��𐔂���A�Ƃ������炢�łȂ��ƁA���H��̖��Ƃ��Ă͕�����Ȃ��C�����܂��B
�Ƃ����ƁA
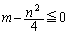 �@����@
�@����@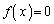 �́A
�́A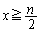 �͈̔͂Ɏ������������܂�(
�͈̔͂Ɏ������������܂�(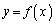 �̎��̈ʒu��
�̎��̈ʒu��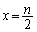 �ł�)�B
�ł�)�B
�E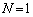 �̂Ƃ��A
�̂Ƃ��A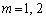 �C
�C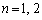 �ł����A���̂����@���݂����g�ݍ��킹�́A
�ł����A���̂����@���݂����g�ݍ��킹�́A 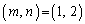 �݂̂ł��B
�݂̂ł��B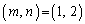 �̂Ƃ��A
�̂Ƃ��A�́A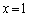 (
(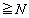 )�����Ɏ����܂��B
)�����Ɏ����܂��B
�������݂���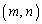 �̑g�́A1�g����܂��B
�̑g�́A1�g����܂��B 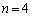 �̂Ƃ��́A
�̂Ƃ��́A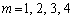 �͂��ׂć@���݂����A
�͂��ׂć@���݂����A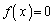 ��
��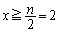 �͈̔͂Ɏ������������܂��B
�͈̔͂Ɏ������������܂��B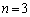 �̂Ƃ��́A
�̂Ƃ��́A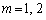 ���@���݂����܂��B
���@���݂����܂��B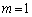 �̂Ƃ��A
�̂Ƃ��A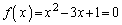 �̉���
�̉���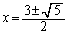 ��
��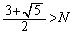 �Ȃ̂ŏ������݂����܂��B
�Ȃ̂ŏ������݂����܂��B
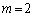 �̂Ƃ��A
�̂Ƃ��A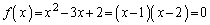 �͎�����2�����̂ŏ������݂����܂��B
�͎�����2�����̂ŏ������݂����܂��B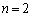 �̂Ƃ��́A
�̂Ƃ��́A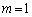 ���@���݂����܂����A
���@���݂����܂����A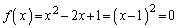 �̎�����1��N��菬�����̂ŏ������݂����܂���B
�̎�����1��N��菬�����̂ŏ������݂����܂���B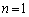 �̂Ƃ��́A�@���݂���m�͂���܂���B
�̂Ƃ��́A�@���݂���m�͂���܂���B�������݂���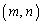 �̑g�́A6�g����܂��B
�̑g�́A6�g����܂��B �����܂łŁA���������߂�Ǝv���܂����A�����@�̂ق��ɁAN�ȏ�̎����������Ƃ����������l����K�v������܂��B���̏����́A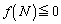 �ł��B
�ł��B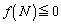 �����������Ƃ��A
�����������Ƃ��A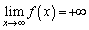 �Ȃ̂ŕ�����
�Ȃ̂ŕ�����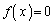 ��
��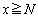 �ƂȂ�������������܂��B����āA
�ƂȂ�������������܂��B����āA
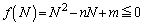
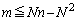 �@����A
�@����A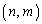 �̐��𐔂��邱�ƂɂȂ�܂��B���E��
�̐��𐔂��邱�ƂɂȂ�܂��B���E��
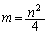 �@����B
�@����B
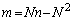 �@����C
�@����C
���A�B���C�̏㑤�ɂ���A���E���B�C�C��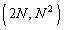 �Őڂ��Ă��܂��B
�Őڂ��Ă��܂��B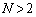 �̂Ƃ���
�̂Ƃ���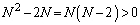 ���
���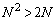 �ƂȂ�A�ړ_��m�̒l��
�ƂȂ�A�ړ_��m�̒l��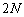 ���傫���A�B�C�C�̐ړ_�́A
���傫���A�B�C�C�̐ړ_�́A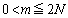 �͈̔͂ɓ���܂���B
�͈̔͂ɓ���܂���B
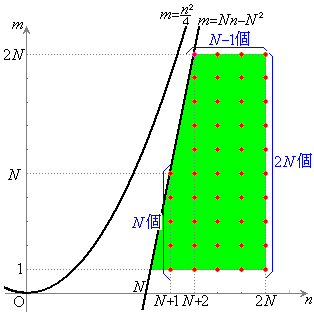 �]���āA
�]���āA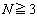 �̂Ƃ��ɂ́A�@���l����K�v�͂Ȃ��A�A����
�̂Ƃ��ɂ́A�@���l����K�v�͂Ȃ��A�A����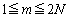 ����
����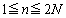 (�E�}���ΐF���F�����̑�`�̈�)���݂�������m�Cn�̑g�𐔂���悢���ƂɂȂ�܂��B
(�E�}���ΐF���F�����̑�`�̈�)���݂�������m�Cn�̑g�𐔂���悢���ƂɂȂ�܂��B
���E���C�́A �C
�C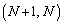 �C
�C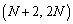 ��ʂ�A
��ʂ�A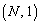 �̉���ʂ�܂��B�̈���̒���
�̉���ʂ�܂��B�̈���̒���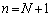 ��ɂ�
��ɂ�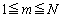 ��N�̊i�q�_(���W�������̓_)������A�u
��N�̊i�q�_(���W�������̓_)������A�u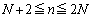 ����
���� 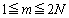 �v�̒����`���ɂ́A
�v�̒����`���ɂ́A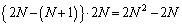 �̊i�q�_������܂��B���킹�āA
�̊i�q�_������܂��B���킹�āA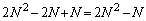 �̊i�q�_������܂��B
�̊i�q�_������܂��B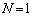 �C
�C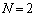 ��������ƁA���������ʂ�^���܂��B
��������ƁA���������ʂ�^���܂��B
�������݂��������̑g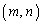 �́A
�́A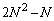 �g ......[��]
�g ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B