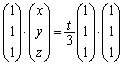�����H�Ƒ�w2009�N�O�����w�������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@�_P���������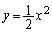 ��2�{�̐ڐ���������Ƃ��A2�̐ړ_��A�CB�Ƃ��A����PA�CPB����т��̕������ň͂܂��}�`�̖ʐς�S�Ƃ���BPA�CPB����������Ƃ���S�̍ŏ��l�����߂�B
��2�{�̐ڐ���������Ƃ��A2�̐ړ_��A�CB�Ƃ��A����PA�CPB����т��̕������ň͂܂��}�`�̖ʐς�S�Ƃ���BPA�CPB����������Ƃ���S�̍ŏ��l�����߂�B
[��]
[2]�@����a�ɑ��A����1���ϊ�
���l����B�ȉ���2�������݂�������L�����݂���悤��a�����߂�B
(1) L�͓_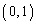 ��ʂ�B
��ʂ�B (2) �_Q��L��ɂ���A����f�ɂ�鑜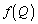 ��L��ɂ���B
��L��ɂ���B [��]
[3]�@N�𐳂̐����Ƃ���B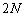 �ȉ��̐��̐���m�Cn����Ȃ�g
�ȉ��̐��̐���m�Cn����Ȃ�g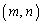 �ŁA������
�ŁA������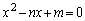 ��N�ȏ�̎����������悤�Ȃ��͉̂��g���邩�B
��N�ȏ�̎����������悤�Ȃ��͉̂��g���邩�B
[��]
[4]�@xyz��Ԃ̌��_�Ɠ_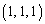 ��ʂ钼����
��ʂ钼����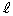 �Ƃ���B
�Ƃ���B
(1) 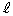 ��̓_
��̓_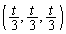 ��ʂ�
��ʂ�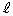 �Ɛ����ȕ��ʂ��Axy���ʂƌ�����Ăł��钼���̕����������߂�B
�Ɛ����ȕ��ʂ��Axy���ʂƌ�����Ăł��钼���̕����������߂�B (2) �s����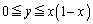 �̕\��xy���ʓ��̗̈��D�Ƃ���B
�̕\��xy���ʓ��̗̈��D�Ƃ���B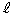 �����Ƃ���D����]�����ē������]�̂̑̐ς����߂�B
�����Ƃ���D����]�����ē������]�̂̑̐ς����߂�B [��]
�e�⌟��
[1](��������)�@2009�N�̓��H������́A�ǂ����A���w�͖��_���o�̂悤�ł��B���������Ƃ��͉p��̏o���ő傫�����E���Ă��܂��̂ŁA���w�ӉȖڂɂ��Ă������ɂ͋C�̓łȂ��ƂɂȂ����̂ł͂Ȃ����Ǝv���܂��B���̋ɂ߂����{��ł��B
2�����ŕ\�����������̈قȂ�2�ڐ��̌�_��x���W���A2�ړ_��x���W�̑������ςɂȂ邱�Ƃ́A�قڏ펯�̂悤�Ȃ��Ƃł��B�����āA����2�ڐ��ƕ������Ƃň͂܂�镔���̖ʐς��A���̌�_��ʂ�x���ɐ����Ȓ�����2�ɕ����Čv�Z���邱�Ƃ�A�ʐόv�Z�ɏo�Ă����ϕ����A
�̂悤�ɂ��Čv�Z���邱�Ƃ��A���H�僌�x���ł���A�m��Ȃ��ł͋�����Ȃ��K�{�Z�I�ł��B
�����������ł��킢�̂́A�P�A���X�E�~�X�ł��B2009�N�̓��H��̐��w�ł́A4�⊮���������ł����Ԃ��]�����ł��傤����A�]�������Ԃłǂ�قǂ�������ƌ��������s�������A�Ƃ������Ƃ��d�v�������Ǝv���܂��B�����̕��̎�����A�ŏI�������I�����Ƃ���ň��S���Ă��܂�Ȃ��ŁA��蕶��1�x�ǂݒ����A��蕶�̗v���ɉ����������Ă��邩���m�F���A���Ȃ��Ƃ����\�b���x�A�̗�����������A�Ƃ����N�Z�����Ă����Ē����������̂ł��B
[2](��������)�@�s��A�̕\��1���ϊ��ɂ�����s���������A�ŗL�l�A�ŗL�x�N�g�����g���čl���Ă݂܂��B
�s��A���ŗL�lα �������A���̌ŗL�l�ɑ���ŗL�x�N�g����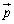 ���Ƃ��܂��B�܂�A
���Ƃ��܂��B�܂�A
���̂Ƃ��A�x�N�g���������F
�ŗ^�����钼��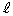 ��̓_�́A
��̓_�́A
���A����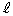 ��Ɉڂ�̂ŁA����
��Ɉڂ�̂ŁA����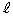 �͂���1���ϊ��ɂ��ĕs�������ɂȂ�܂��B����
�͂���1���ϊ��ɂ��ĕs�������ɂȂ�܂��B����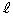 �͌��_��ʂ钼���ł��B
�͌��_��ʂ钼���ł��B
���x�́A�s��A�̕\��1���ϊ������_��ʂ�Ȃ��s������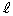 �����Ƃ��܂��B���_��ʂ�����x�N�g����
�����Ƃ��܂��B���_��ʂ�����x�N�g����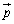 �̒����ƒ���
�̒����ƒ���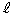 �Ƃ̌�_�̈ʒu�x�N�g���́As��0�łȂ������Ƃ��āA
�Ƃ̌�_�̈ʒu�x�N�g���́As��0�łȂ������Ƃ��āA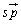 �ƕ\���܂��B�s������
�ƕ\���܂��B�s������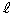 �̕����x�N�g����
�̕����x�N�g����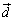 �Ƃ���ƁA
�Ƃ���ƁA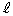 �̃x�N�g���������́At�������̕ϐ��Ƃ��āA
�̃x�N�g���������́At�������̕ϐ��Ƃ��āA
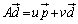 (u�Cv�͎���)�Ƃ��āA
(u�Cv�͎���)�Ƃ��āA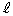 ��̓_��1���ϊ��ɂ��A
��̓_��1���ϊ��ɂ��A
�Ɉڂ�܂����A���ꂪ����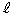 ��̓_�ł��邽�߂ɂ́A
��̓_�ł��邽�߂ɂ́A
���ꂪ�A�C�ӂ̎���t�ɂ�����炸�������邽�߂ɂ́A�P�����̏������A
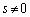 ���A
���A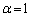 �C�܂��A
�C�܂��A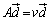 �ƂȂ�܂��B
�ƂȂ�܂��B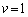 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A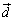 ���ŗL�l1�ɑ���ŗL�x�N�g���ƂȂ��Ă��܂��̂ŁA�ʂɍl����K�v������܂�(��q)�B
���ŗL�l1�ɑ���ŗL�x�N�g���ƂȂ��Ă��܂��̂ŁA�ʂɍl����K�v������܂�(��q)�B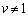 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A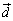 ��
��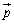 ��1���Ɨ��ŁA1���ϊ������_��ʂ�Ȃ��s������
��1���Ɨ��ŁA1���ϊ������_��ʂ�Ȃ��s������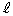 �����Ƃ��A�s��A�͌ŗL�l1�������A����1�A1�ȊO�̌ŗL�lv�����ĂA�s������
�����Ƃ��A�s��A�͌ŗL�l1�������A����1�A1�ȊO�̌ŗL�lv�����ĂA�s������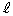 �̕����x�N�g���́Av�ɑ���ŗL�x�N�g���ɂȂ�܂��B
�̕����x�N�g���́Av�ɑ���ŗL�x�N�g���ɂȂ�܂��B
�s�������͑����̖��ł͌��_��ʂ钼���ɂȂ�̂ł����A���嗝�n'82[1]�Ɏ��̖�肪����܂��B
�s��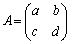 �ɂ���Ē�܂�xy���ʂ�1���ϊ���f�Ƃ���B���_�ȊO�̂���_P��f�ɂ����P���g�ɂ������Ȃ�A���_��ʂ�Ȃ�����
�ɂ���Ē�܂�xy���ʂ�1���ϊ���f�Ƃ���B���_�ȊO�̂���_P��f�ɂ����P���g�ɂ������Ȃ�A���_��ʂ�Ȃ�����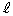 �ł����āA
�ł����āA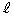 �̂ǂ̓_��f�ɂ����
�̂ǂ̓_��f�ɂ����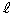 �̓_�ɂ������悤�Ȃ��̂����݂��邱�Ƃ��ؖ�����B
�̓_�ɂ������悤�Ȃ��̂����݂��邱�Ƃ��ؖ�����B
���_�ȊO�̕s���_P�����݂���Ƃ��A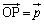 �Ƃ��āA
�Ƃ��āA
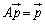 �@����@
�@����@
�ł����A�t�s��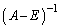 �����݂���Ƃ��ɂ́A������
�����݂���Ƃ��ɂ́A������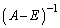 ��������ƁA
��������ƁA
�ƂȂ��āAP�����_�Ɍ����Ă��܂��̂ŁA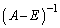 �͑��݂����A
�͑��݂����A
�łȂ���Ȃ�܂���B����́A�ŗL�������F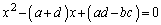 ��
��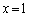 ���������0�ɂȂ�Ƃ������ƂŁA�s��A�͌ŗL�l1�������܂��B���̂Ƃ��A�s��A�̂���1�̌ŗL�l��k�Ƃ��āA
���������0�ɂȂ�Ƃ������ƂŁA�s��A�͌ŗL�l1�������܂��B���̂Ƃ��A�s��A�̂���1�̌ŗL�l��k�Ƃ��āA
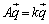 �@����A
�@����A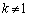 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A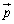 ��
��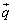 ��1���Ɨ��ł��B�Ȃ��Ȃ�A
��1���Ɨ��ł��B�Ȃ��Ȃ�A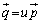 (u�͎���)�Ə������Ƃ���ƁA
(u�͎���)�Ə������Ƃ���ƁA
�Ƃ��������������邩��ł��B
���̂Ƃ��As��C�ӂ̎����̒萔�Ƃ��āA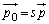 �Ƃ���ƁA�x�N�g���������F
�Ƃ���ƁA�x�N�g���������F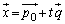 �ŗ^�����钼��
�ŗ^�����钼��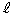 (���_��ʂ�Ȃ�)���l����ƁA
(���_��ʂ�Ȃ�)���l����ƁA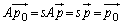 ���A
���A
�ƂȂ�A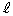 ��̓_��
��̓_��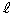 ��Ɉڂ邱�Ƃ��킩��܂�(�O�q�̂悤�ɁA
��Ɉڂ邱�Ƃ��킩��܂�(�O�q�̂悤�ɁA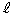 �͕s�������ł�)�B
�͕s�������ł�)�B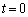 �̂Ƃ��A
�̂Ƃ��A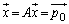 �Ȃ̂ŁA�ʒu�x�N�g����
�Ȃ̂ŁA�ʒu�x�N�g����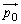 �ƂȂ�_�͕s���_�ł��B
�ƂȂ�_�͕s���_�ł��B
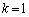 �̏ꍇ(�ŗL�l1���d��)�ɂ́A
�̏ꍇ(�ŗL�l1���d��)�ɂ́A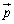 ��1���Ɨ��ȃx�N�g����
��1���Ɨ��ȃx�N�g����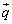 (���ł��悢)�Ƃ��āA
(���ł��悢)�Ƃ��āA
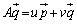 �@����B
�@����B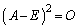 �Ȃ̂ŁA
�Ȃ̂ŁA
�ƂȂ�͂��ł����A
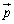 �C
�C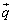 ��1���Ɨ��Ȃ̂ŁA
��1���Ɨ��Ȃ̂ŁA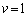 �C�B���A
�C�B���A
������A�x�N�g���������F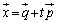 �ŗ^�����钼��
�ŗ^�����钼��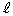 (���_��ʂ�Ȃ�)���l����ƁA
(���_��ʂ�Ȃ�)���l����ƁA
�ƂȂ�A��͂�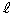 ��̓_��
��̓_��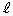 ��Ɉڂ�܂��B�A���A
��Ɉڂ�܂��B�A���A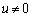 �̂Ƃ��ɂ́A�C�ӂ�t�ɂ���
�̂Ƃ��ɂ́A�C�ӂ�t�ɂ���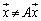 �Ȃ̂ŁA�s���_�͑��݂��܂���B
�Ȃ̂ŁA�s���_�͑��݂��܂���B
����̖��ł͕s���_�����݂��܂������A���H��̖{��̏���(1)��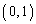 ���s���_�ł���A�s��
���s���_�ł���A�s��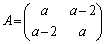 ���ŗL�l1��������
���ŗL�l1��������
���A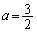 �̂Ƃ��ɁA���嗝�n'82[1]�̖�蕶�ɂ��A�������݂�������L�����݂��܂��B���̂Ƃ��A
�̂Ƃ��ɁA���嗝�n'82[1]�̖�蕶�ɂ��A�������݂�������L�����݂��܂��B���̂Ƃ��A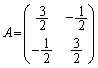 �ł����A
�ł����A
���AA�͌ŗL�l1�C2�������܂��B
���A�ŗL�l1�ɑ���ŗL�x�N�g����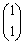
���A�ŗL�l2�ɑ���ŗL�x�N�g����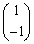
�ŗL�l1���d���ł͂Ȃ��̂ŁA�s�������́As��C�ӂ̎����̒萔�At�������̕ϐ��Ƃ��āA�x�N�g���������F
�ŗ^�����܂��Bt���������āA
���ꂪ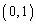 ��ʂ�Ƃ��A
��ʂ�Ƃ��A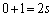 ���
���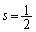 �C�s�������́A
�C�s�������́A
�ƂȂ�܂��B
���H��̖��̍s��A���ŗL�l1���d���ɂ����Ƃ͂���܂��A�ŗL�l1���d���ɂ��s��A�Ⴆ�A
�̕s���������l���Ă݂܂��B
���A�ŗL�l1�ɑ���ŗL�x�N�g����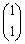
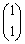 ��1���Ɨ��ȃx�N�g���A�Ⴆ��
��1���Ɨ��ȃx�N�g���A�Ⴆ��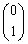 �������Ă���ƁA�s�������́A�x�N�g���������F
�������Ă���ƁA�s�������́A�x�N�g���������F
�ŗ^�����܂��Bt����������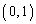 ��ʂ�s�������́A
��ʂ�s�������́A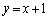 �ɂȂ�܂��B���̏ꍇ�ɂ́A�s��A�̕\��1���ϊ��ɂ��s��������̓_
�ɂȂ�܂��B���̏ꍇ�ɂ́A�s��A�̕\��1���ϊ��ɂ��s��������̓_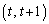 ��
��
���A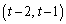 �Ɉڂ�̂ŁA�s���_�͑��݂��܂���B
�Ɉڂ�̂ŁA�s���_�͑��݂��܂���B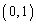 ��ʂ�s�������͑��݂��܂��B
��ʂ�s�������͑��݂��܂��B
��L�ȊO�̏ꍇ�ł́A�s�����������_�ȊO�̓_��ʉ߂���ꍇ�͂���܂���B�]���āA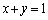 �ȊO��
�ȊO��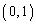 ��ʉ߂���s�����������݂���A���̕s�������́A���_��ʉ߂��邱�ƂɂȂ�܂��B
��ʉ߂���s�����������݂���A���̕s�������́A���_��ʉ߂��邱�ƂɂȂ�܂��B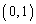 �ƌ��_��ʉ߂��钼����
�ƌ��_��ʉ߂��钼����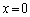 (y��)�ł��B�ŏ��̕��ɏ������悤�ɁA���̂Ƃ��A�s��A�͌ŗL�x�N�g��
(y��)�ł��B�ŏ��̕��ɏ������悤�ɁA���̂Ƃ��A�s��A�͌ŗL�x�N�g��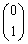 �������܂��B
�������܂��B
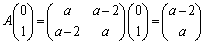 //
// 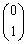
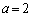 �̂Ƃ��ɂ��A�������݂�������L�����݂��܂��B
�̂Ƃ��ɂ��A�������݂�������L�����݂��܂��B
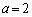 �̂Ƃ��A
�̂Ƃ��A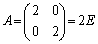 �ł�(�s��A�͑Ίp�����݂̂������A�������2�Ȃ̂ŁA�d���̌ŗL�l2�������܂�)���A�C�ӂ̃x�N�g��
�ł�(�s��A�͑Ίp�����݂̂������A�������2�Ȃ̂ŁA�d���̌ŗL�l2�������܂�)���A�C�ӂ̃x�N�g��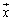 �ɂ��āA
�ɂ��āA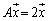 �ƂȂ�̂ŁA���́A�ŗL�x�N�g���͔C�ӂ̃x�N�g���ɂȂ��Ă��܂��B�܂�A���_��ʂ�C�ӂ̒������s�������ɂȂ�܂��B
�ƂȂ�̂ŁA���́A�ŗL�x�N�g���͔C�ӂ̃x�N�g���ɂȂ��Ă��܂��B�܂�A���_��ʂ�C�ӂ̒������s�������ɂȂ�܂��B
�Q�l�܂łɁA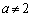 �̂Ƃ��ɂ́A�ŗL�������F
�̂Ƃ��ɂ́A�ŗL�������F
���AA�͈قȂ�2�̌ŗL�l2�C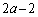 (
(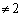 )�������܂��B
)�������܂��B
���A�ŗL�l2�ɑ���ŗL�x�N�g���́A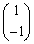
���A�ŗL�l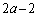 �ɑ���ŗL�x�N�g���́A
�ɑ���ŗL�x�N�g���́A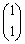
���̂Ƃ��ɂ́A���_��ʂ钼���F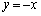 �C
�C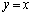 ���s������(�_
���s������(�_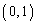 �͒ʂ�܂���)�ɂȂ�܂��B
�͒ʂ�܂���)�ɂȂ�܂��B
��������ƁA���_�ȊO�̓_P��ʉ߂��A���_��ʂ�Ȃ��s�����������݂���̂́A
(i) �s��A���d���łȂ��ŗL�l1�����Ƃ��A��������̌ŗL�l�ɑ�����ŗL�x�N�g���ɕ��s�Ȓ����œ_P��ʉ߂��钼�����s�������ɂȂ�B�_P�͕s���_�ɂȂ�B
(ii) �s��A�̌ŗL�l1���d���ɂȂ�Ƃ��A�ŗL�x�N�g���ɕ��s�Ȓ����œ_P��ʉ߂��钼�����s�������ɂȂ�B�_P�͕s���_�ł͂Ȃ��B
�̏ꍇ�ŁA
(iii) �s��A���ŗL�l1�������Ȃ��Ƃ��ɂ́A�s�������͌��_��ʂ�B
���H��̖{��̏ꍇ�ł���A(i)�̏ꍇ��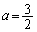 �C(ii)�̏ꍇ�͂Ȃ��A(iii)�̏ꍇ��
�C(ii)�̏ꍇ�͂Ȃ��A(iii)�̏ꍇ��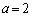 �Ƃ������ƂɂȂ�܂��B
�Ƃ������ƂɂȂ�܂��B
[3](��������)�@��蕶����ǂ�������ł́A�i�q�_�𐔂������2���������̉��̔z�u�������ł��Ă����ɂ����G�����Ɍ����܂��B�ł́A�����������̏퓅��i�ŁA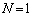 �C
�C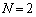 �̏ꍇ���l���A����������ł����ʉ�����A�Ƃ������j�ł���Ă���܂��B�K�v�Ȃ�A
�̏ꍇ���l���A����������ł����ʉ�����A�Ƃ������j�ł���Ă���܂��B�K�v�Ȃ�A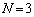 �C
�C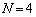 �ƃO���t��`���Ȃ���A�i�q�_�̐��𐔂��Ă��ǂ������m��܂���B
�ƃO���t��`���Ȃ���A�i�q�_�̐��𐔂��Ă��ǂ������m��܂���B
�������Ȃ���A2����������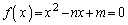 �Ƃ��āA�������̎��̈ʒu
�Ƃ��āA�������̎��̈ʒu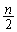 ���A
���A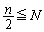 �����Ă��Ď��̉E�������l����悢���ƁA����ɂ́Anm���ʏ�ŁA
�����Ă��Ď��̉E�������l����悢���ƁA����ɂ́Anm���ʏ�ŁA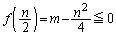 �̋��E��
�̋��E��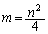 ���AN�ȏ�̉����������F
���AN�ȏ�̉����������F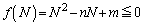 �̋��E��
�̋��E��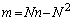 �����ɗ��Ă��܂����Ƃ��킩���Ă��܂����Ƃ���Ŕ��q�������܂��B���H��̎������ł��A���������ȁA�����̊ԈႢ�ł́H�Ǝv���āA�������x���ǂݕԂ����������Ȃ��炸�����Ǝv���܂��B
�����ɗ��Ă��܂����Ƃ��킩���Ă��܂����Ƃ���Ŕ��q�������܂��B���H��̎������ł��A���������ȁA�����̊ԈႢ�ł́H�Ǝv���āA�������x���ǂݕԂ����������Ȃ��炸�����Ǝv���܂��B
�o��҂����������Ⴂ�����̂��A�����Ґ��𑝂₷���߂Ɏ��������Ӑ}�I�ɈՂ��������̂��A�ƁA����ʋ^���������Ă��܂��܂��B
���ǁA��`��̈���̊i�q�_�̐��𐔂���(�������A��v�_���i�q�_�ɂȂ��Ă��ďꍇ�����̕K�v���Ȃ�)�����̂��ƂŁA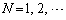 �Ȃǂƍl����K�v����Ȃ��A�ŏ������ʓI�ɍl���Ă��[���ł��܂��B
�Ȃǂƍl����K�v����Ȃ��A�ŏ������ʓI�ɍl���Ă��[���ł��܂��B
�����������ł��킢�̂́A�ꌩ�A���G�����Ɍ�����̂Ŏ������Ƀp�X���A�����I����ɁA�ȂA�ȒP�������A�ƋC�Â����Ƃł��B2009�N�x�̓��H������̏ꍇ�́A�قƂ�ǂ̎������Ԃ�]�����Ǝv����̂ŁA���̖����p�X���ė܂������͏��Ȃ��Ǝv���܂����A�������ɂ�炸�Ղ�����������̂Œ��ӂ��Ă��������B
[4](��������)�@�Ղ�������2009�N�x�O���̓��H��̐��w�̖��̒��ł́A�n�C���x���Ȗ��ł��B�ł����A�悭�����Ă��ĉ�]�̂̑̐ς̊�{���������肵�Ă�����ɂƂ��Ă͉��ł��Ȃ��v�Z��肾�����Ǝv���܂��B(1)�̗U�����Ȃ���l�����ނ��Ƃ����邩���m��܂��A(1)�����ɓK�ȃq���g�ɂȂ��Ă��āA�肪�~�܂邱�Ƃ��Ȃ������������������Ǝv���܂��B
(1)�ł́A���ʂ̕������̒m��������ƕ֗��ł����A�m��Ȃ��Ă��A�ȉ��̂悤�ɂ���Γ��l�̑Ώ����ł��܂��B�ł́A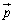 �C
�C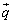 �����_�Ɠ_
�����_�Ɠ_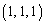 ��ʂ钼���ɐ����ȃx�N�g���Ƃ��āA���ʂ̃x�N�g���������F
��ʂ钼���ɐ����ȃx�N�g���Ƃ��āA���ʂ̃x�N�g���������F
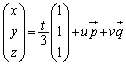 �@���(��)
�@���(��)
���l���A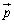 �C
�C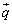 ��
��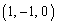 �C
�C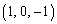 �ȂǂƋ�̂ɑz�肵�Ė����l���Ă��܂����A
�ȂǂƋ�̂ɑz�肵�Ė����l���Ă��܂����A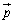 �C
�C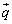 �̓x�N�g��
�̓x�N�g��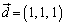 �ɐ����Ȃ̂ŋ�̓I�ɋ��߂Ȃ��Ă�(��)�̎��_�ŁA���ӂ�
�ɐ����Ȃ̂ŋ�̓I�ɋ��߂Ȃ��Ă�(��)�̎��_�ŁA���ӂ�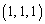 �Ƃ̓��ς��Ƃ��Ă��܂��A
�Ƃ̓��ς��Ƃ��Ă��܂��A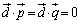 �Ȃ̂ŁA
�Ȃ̂ŁA
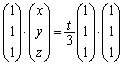
�� 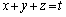
�ƂȂ��ĕ��ʂ̕��������o�Ă��܂��B������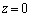 �Ƃ���A
�Ƃ���A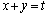 �Ƃ��������̕������������܂��B
�Ƃ��������̕������������܂��B
(2)�ł́Axy���ʏ�̗̈����]����ƌ����Ă��A��]���ɐ����ȕ��ʂƂ̌����ƂȂ��������]�������̂��l����悢�A���̐�����(1)�ŋ��߂Ă���̂��A�ƁA�킩���Ă��܂����Ƃ͐ϕ��̌v�Z���ł��B
���ǁA��������]���悤�ƁA�Ȑ�����]���悤�ƁA�L����������ʐ}�`����]���悤�ƁA���̂���]���悤�ƁA��邱�Ƃ͓����ŁA��]���ɐ����ȕ��ʂʼn�]�̂��Ƃ��A��]������ł������_�ƍł��߂��_��T���o���A���Ƃ́A�O���̉~��������̉~����菜�������̂��Ƃł��B
�ӗ~�I�Ȏ��̒��ɂ́A������p�^�[���̖��������āA�����̓��̒��ŁA���̃p�^�[���͉�@A�C���̃p�^�[���͉�@B�C�����������ό`�����Ɖ�@B�_�b�V���A�Ƃ�����ɁA�p�^�[�����ƂɊ��S�ɐ������邱�Ƃ�ڕW�ɂ��悤�Ɗ撣��l�����܂��B�ł����A���Ɍ��킹�����̓��_�ȓw�͂ł��B��]�̂̑̐ς����߂����1������Ƃ��ɁA�����A��������]����̂ł͂Ȃ��A�}�`����]����̂�������ǂ��Ȃ�̂��낤�A���̂�������ǂ��Ȃ�̂��낤�ƁA���W�����čl���Ă����A5��̖����������Ԃ��A�����̎��N���u������{�����e�B�A�����A���邢�͊w���Ղ̏����Ɏg�����Ƃ��ł��܂��B�����āA5��̖���������5�̃p�^�[���̈ËL�ŕЕt���悤�Ƃ�������A������ł͂邩�ɉ��p�������悤�ɂȂ�̂ł��B
�������A���w�̕��ł��傫�ȃE�F�C�g���߂�̂͂�͂��b�����̈ËL���Ǝv���܂��B��]�̂̑̐ς��ǂ����߂邩�A�u���ϕ����ǂ����邩�A�u���ϕ��̃p�^�[���A�ȂǁA�ËL�̕K�v�Ȃ��Ƃ͂����������܂��B�ł����A�ËL�̕��ʂ��ł�����茸�炷�w�͂��s���A�t��搉̂��鎞�Ԃ��m�ۂ��邱�Ƃ��l����ׂ��ł��B���Љ�ɏo�Ă�����A�}�j���A���ʂ�ɕЕt���Ȃ��ɂ����Α������܂��B���������Ƃ��ɁA�}�j���A���̃p�^�[���̒��ɂȂ���������ł��Ȃ������ł͍����Ă��܂��ꍇ���o�Ă��܂��B�ނ���A���Ɍ��炸�A�����̍s���̃p�^�[�����L���Ă������Ƃ̕����d�v�������肷��̂ł��B�����̂������玩���������Ă����@���C�u�����̒��ŕЕt���Ȃ����ɏo���킵���Ƃ��ɂǂ��Ώ����邩�A�Ƃ����g���[�j���O�����Ă����̂͑�Ȃ��Ƃł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 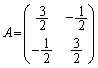 �ł����A
�ł����A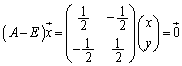
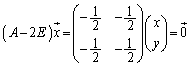
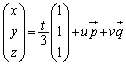 �@���(��)
�@���(��)