���H�吔�w'09�N�O��[1]
�_P���������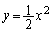 ��2�{�̐ڐ���������Ƃ��A2�̐ړ_��A�CB�Ƃ��A����PA�CPB����т��̕������ň͂܂��}�`�̖ʐς�S�Ƃ���BPA�CPB����������Ƃ���S�̍ŏ��l�����߂�B
��2�{�̐ڐ���������Ƃ��A2�̐ړ_��A�CB�Ƃ��A����PA�CPB����т��̕������ň͂܂��}�`�̖ʐς�S�Ƃ���BPA�CPB����������Ƃ���S�̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�p�o�^�C�v�̖��ŗ��Ƃ��Ȃ����ł��B
�_P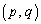 �C2�ړ_��A
�C2�ړ_��A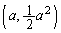 �CB
�CB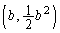 (
(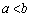 )�Ƃ��܂��B
)�Ƃ��܂��B
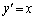 ���A
���A
A�ɂ�������������ڐ��́A
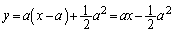 �@����@
�@����@
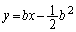 �@����A
�@����A
�@�C�A��A�����āA
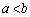 ���A
���A
���ꂪP��x���W�ŁA
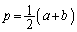 �@����C�@(������A
�@����C�@(������A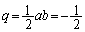 �ƂȂ�܂�)
�ƂȂ�܂�)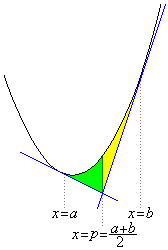 �������͉��ɓʂȂ̂ŁA�ڐ��͕��������牺���ɂ��܂��B����PA�CPB����т��̕������ň͂܂��}�`��
�������͉��ɓʂȂ̂ŁA�ڐ��͕��������牺���ɂ��܂��B����PA�CPB����т��̕������ň͂܂��}�`��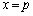 �̂Ƃ���ŕ����čl���܂��B��ϕ��͏��X�H�v���Čv�Z����ƃ��N�ɂȂ�̂ŁA�ȉ��̌v�Z�v�̂��o���Ă��������B
�̂Ƃ���ŕ����čl���܂��B��ϕ��͏��X�H�v���Čv�Z����ƃ��N�ɂȂ�̂ŁA�ȉ��̌v�Z�v�̂��o���Ă��������B
��ϕ�����2��̌`�ɂ������Ƃɒ��ӂ��Ă��������B�����ł���̂́A�������Ɛڐ��Ƃŋ��܂�Ă��镔���̖ʐς��v�Z���Ă��邩��ŁA�@�ƕ������̕������A�A�ƕ������̕����������ꂼ��A�������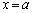 �C
�C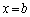 ���d���ɂȂ邩��ł��B��ϕ��̐ϕ��͈͂�a�Cb���o�Ă���̂ŁA�ϕ��v�Z�����N�ɂȂ�܂��B
���d���ɂȂ邩��ł��B��ϕ��̐ϕ��͈͂�a�Cb���o�Ă���̂ŁA�ϕ��v�Z�����N�ɂȂ�܂��B
�B�C�C������̂őΏ̎��̋Z�I���g�������̂ł����A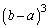 �͑Ώ̎��ł͂���܂���B�ł����A
�͑Ώ̎��ł͂���܂���B�ł����A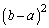 �Ȃ�Ώ̎��ł��B�����ŁA
�Ȃ�Ώ̎��ł��B�����ŁA
�ƕό`���āA�B�C�C���g���ƁA
����́A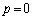 �̂Ƃ��ɍŏ��ƂȂ�AS�̍ŏ��l�́A
�̂Ƃ��ɍŏ��ƂȂ�AS�̍ŏ��l�́A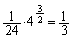 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B