���H�吔�w'09�N�O��[4]
xyz��Ԃ̌��_�Ɠ_ ��ʂ钼����
��ʂ钼����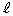 �Ƃ���B
�Ƃ���B
(1) 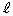 ��̓_
��̓_ ��ʂ�
��ʂ�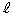 �Ɛ����ȕ��ʂ��Axy���ʂƌ�����Ăł��钼���̕����������߂�B
�Ɛ����ȕ��ʂ��Axy���ʂƌ�����Ăł��钼���̕����������߂�B (2) �s����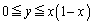 �̕\��xy���ʓ��̗̈��D�Ƃ���B
�̕\��xy���ʓ��̗̈��D�Ƃ���B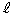 �����Ƃ���D����]�����ē������]�̂̑̐ς����߂�B
�����Ƃ���D����]�����ē������]�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ή�]���̋�ԔłƂ������ƂŃM�����Ƃ������܂����A(1)�����͂ȃq���g�ɂȂ��Ă��ĕ��j�𗧂Ă₷���Ȃ��Ă��܂��B
(1) ���s�ے��͈̔͊O�ł����A���ʂ̕�������m���Ă���A�@���x�N�g���� �ł��镽�ʂ̕������́A
�ł��镽�ʂ̕������́A �Ƃ����āA���ʂ��_ ��ʂ�Ƃ��A
��ʂ�Ƃ��A  �@��
�@�� 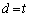
����āA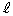 �ɐ�����
�ɐ����� ��ʂ镽��π�̕������́A
��ʂ镽��π�̕������́A xy����(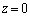 )�ƌ�����Ăł��钼���́A
)�ƌ�����Ăł��钼���́A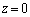 �Ƃ��āA
�Ƃ��āA �ƁA�ȒP�ɋ��߂邱�Ƃ��ł��܂��B
���s�͈͂ōl����̂ł���A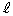 �ɐ�����
�ɐ����� ��ʂ镽��π��̓_
��ʂ镽��π��̓_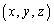 �ɂ��āA
�ɂ��āA ����π�� �Ɛ����Ȃ̂ŁA
�Ɛ����Ȃ̂ŁA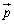 �C
�C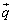 ��
��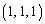 �Ɛ����B
�Ɛ����B �C
�C ��
��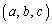 �Ƃ����ƁA
�Ƃ����ƁA
 �@(�������Q��)�������1���Ɨ��ȃx�N�g����2���܂��B�Ⴆ�A
�@(�������Q��)�������1���Ɨ��ȃx�N�g����2���܂��B�Ⴆ�A ��I��(���ɂ��l�����܂�)�ƁA
��I��(���ɂ��l�����܂�)�ƁA ����π�F �@����@
�@����@ �@��xy���ʂƂ̌���������߂邽�߂ɁA�@�ɂ����āA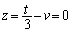 �Ƃ���ƁA
�Ƃ���ƁA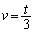
���̂Ƃ��A u���������邽�߂ɁA���ӂ�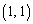 �Ƃ̓��ς����ƁA
�Ƃ̓��ς����ƁA 
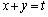 ......[��]
......[��]
(2) ��]�̂��̐��́A��]��(����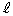 )�ɐ����ȕ���π�ʼn�]�̂�����Ƃ��ɂł���f�ʂ̖ʐ�
)�ɐ����ȕ���π�ʼn�]�̂�����Ƃ��ɂł���f�ʂ̖ʐ�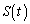 ����]���ɉ����Đϕ����邱�Ƃɂ���ċ��߂邱�Ƃ��ł��܂��B
����]���ɉ����Đϕ����邱�Ƃɂ���ċ��߂邱�Ƃ��ł��܂��B �܂��A ���̈�D��
���̈�D��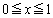 �͈̔͂ɑ��݂��Ă��邱�Ƃɒ��ӂ��܂��B�܂��A������
�͈̔͂ɑ��݂��Ă��邱�Ƃɒ��ӂ��܂��B�܂��A������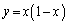 ��
�� �ɂ������ڐ��̌X����1�ł����ĕ������͏�ɓʂȂ̂ŁA����
�ɂ������ڐ��̌X����1�ł����ĕ������͏�ɓʂȂ̂ŁA����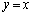 ���܂�xy���ʂɐ����ȕ��ʂ��z���ĉ�]�̂��݂͂������Ƃ͂���܂���B�܂��A��������
���܂�xy���ʂɐ����ȕ��ʂ��z���ĉ�]�̂��݂͂������Ƃ͂���܂���B�܂��A�������� �ɂ�����ڐ��̌X����
�ɂ�����ڐ��̌X���� �Ȃ̂ŁA
�Ȃ̂ŁA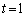 �̂Ƃ��̕���π���z���ĉ�]�̂��݂͂������Ƃ�����܂���B
�̂Ƃ��̕���π���z���ĉ�]�̂��݂͂������Ƃ�����܂���B
�����ŁA����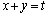 �Ɨ̈�D�̋��E���Ƃ̌�_�ׂĂ����܂��B
�Ɨ̈�D�̋��E���Ƃ̌�_�ׂĂ����܂��B
����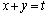 ��x���Ƃ̌�_��
��x���Ƃ̌�_��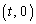
���� ��
�� �Ƃ̌�_�́A
�Ƃ̌�_�́A ���̂Ƃ��A
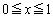 ���A
���A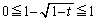 �C
�C
����āA���� �Ɨ̈�D�����������̂́A
�Ɨ̈�D�����������̂́A �̂Ƃ��ł��B
�̂Ƃ��ł��B
����π�Ɨ̈�D�Ƃ̌����̕����́A���� ��
�� �̕����̐����ł��B���̐�����
�̕����̐����ł��B���̐����� �̂܂��ɉ�]����ƁA������̓_�ŁA��]�̒��S
�̂܂��ɉ�]����ƁA������̓_�ŁA��]�̒��S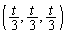 ����ł������_��
����ł������_�� �C�ł��߂��_��
�C�ł��߂��_��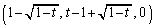 �Ȃ̂ŁA���̂Ƃ��ɂł���}�`�̖ʐ�
�Ȃ̂ŁA���̂Ƃ��ɂł���}�`�̖ʐ� �́A
�́A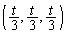 ��
��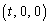 �Ƃ̋���
�Ƃ̋���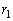 �a�Ƃ���~�̖ʐς���A
�a�Ƃ���~�̖ʐς���A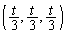 ��
��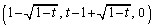 �Ƃ̋����a
�Ƃ̋����a �Ƃ���~�̖ʐς����������̂ɂȂ�܂��B
�Ƃ���~�̖ʐς����������̂ɂȂ�܂��B��  ���_O�Ɠ_
���_O�Ɠ_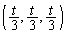 �Ƃ̋�����s (��]��
�Ƃ̋�����s (��]��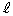 �ɉ����đ��������_���畽��π�܂ł̋���)�Ƃ��āA
�ɉ����đ��������_���畽��π�܂ł̋���)�Ƃ��āA ��]�̂̑̐�V�́A ��
��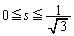 �͈̔͂�s�Ɋւ��Đϕ��������̂ɂȂ�A
�͈̔͂�s�Ɋւ��Đϕ��������̂ɂȂ�A s�̐ϕ����D�ɂ����t�̐ϕ��ɕς��܂�(�u���ϕ����Q��)�B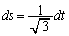
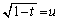 �Ƃ����ƁA
�Ƃ����ƁA �C
�C �Ct�F
�Ct�F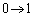 �̂Ƃ��Au�F
�̂Ƃ��Au�F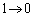
�܂��A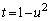
�� 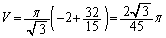 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 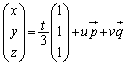
 �@����@
�@����@