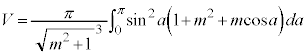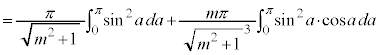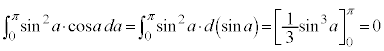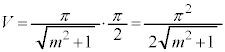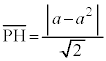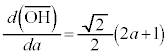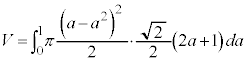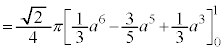�Ή�]���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A�s��ϕ��̌����Ax���̂܂��̉�]�����Q�Ƃ��Ă��������B
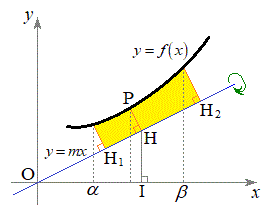 �Ȑ�
�Ȑ�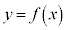 ��
��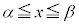 �̕����ƁA����
�̕����ƁA����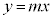 �ƁA2�_
�ƁA2�_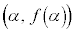 �C
�C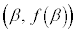 (
(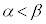 )����e�X����
)����e�X����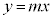 �ɉ��낵�������Ƃň͂܂�镔��(�E�}�ʼn��F�ɓh��ꂽ����)���A����
�ɉ��낵�������Ƃň͂܂�镔��(�E�}�ʼn��F�ɓh��ꂽ����)���A����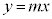 �̉���1��]���Ăł����]��K�̑̐�V�����߂Ă݂܂��B
�̉���1��]���Ăł����]��K�̑̐�V�����߂Ă݂܂��B
x���̂܂��̉�]�̂̑̐ς����߂�̂Ɠ��l�ɁA��]���ɐ����Ȓf�ʂŐ����Ƃ��̒f�ʂ̉~�̖ʐς���]���̕����ɐϕ����邱�Ƃɂ��̐ς����߂܂��B
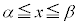 �Ƃ��āA�Ȑ�
�Ƃ��āA�Ȑ�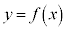 ���1�_P
���1�_P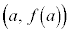 ��ʂ�A����
��ʂ�A����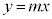 �@����@ �ɐ����Ȓ����́A�X����
�@����@ �ɐ����Ȓ����́A�X����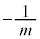 �Ȃ̂ŁA
�Ȃ̂ŁA
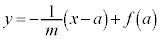 �@����A
�@����A
�@�C�A��A�����āA2�����̌�_H��x���W�����߂�ƁA
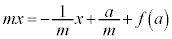
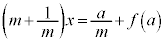
�� 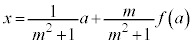 �@����B
�@����B
�_P�Ɠ_H�̋����́A�_P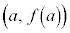 ���璼��
���璼��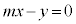 �ɉ��낵�������̒����Ƃ��āA�_�ƒ����̋����̌�����p����ƁA
�ɉ��낵�������̒����Ƃ��āA�_�ƒ����̋����̌�����p����ƁA
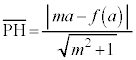
���ꂪ�A�_P��ʂ蒼��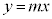 �ɐ����Ȓf�ʂʼn�]��K������Ƃ��̒f�ʂɂł���~�̔��a�ɂȂ�܂��B
�ɐ����Ȓf�ʂʼn�]��K������Ƃ��̒f�ʂɂł���~�̔��a�ɂȂ�܂��B
�f�ʂ̉~�̖ʐς́A �ł��B
�ł��B
���āA�~�̖ʐ� ����]���ɉ����Đϕ�����悢�̂ł����A���̉�]���ɉ��������W�Ƃ��ẮAx���W�Cy���W�ȂǂƓ��l�ɁA���_O����H�܂ł̋���
����]���ɉ����Đϕ�����悢�̂ł����A���̉�]���ɉ��������W�Ƃ��ẮAx���W�Cy���W�ȂǂƓ��l�ɁA���_O����H�܂ł̋��� �����W�Ƃ��čl���܂��B
�����W�Ƃ��čl���܂��B
�_H����x���ɐ���HI�����낵�A���p�O�p�`OHI�ɎO�����̒藝��K�p����ƁA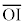 �F
�F �F
�F �� 1�Fm�F
�� 1�Fm�F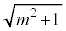
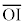 �͇B�ŋ��߂��A�_H��x���W�ł��B����āA
�͇B�ŋ��߂��A�_H��x���W�ł��B����āA
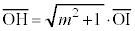
�@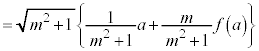
�@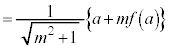 �@����C
�@����C
���߂�̐�V�́A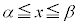 ���A
���A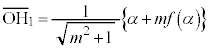 �C
�C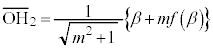 �Ƃ��āA
�Ƃ��āA
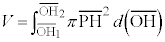
�ł����A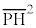 ��a�̊��̌`�ŗ^�����Ă��āA���̂܂܂ł́A
��a�̊��̌`�ŗ^�����Ă��āA���̂܂܂ł́A �ɂ��Đϕ����邱�Ƃ��ł��܂���B
�ɂ��Đϕ����邱�Ƃ��ł��܂���B
�����ŁA�C����p�����u���ϕ����܂��B
�C����a�ɂ��Ĕ�������ƁA
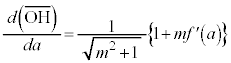
�����ŁA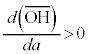 �Ƃ��܂��B�܂�A
�Ƃ��܂��B�܂�A ��a�ɂ��ĒP���������Ƃ��܂��B
��a�ɂ��ĒP���������Ƃ��܂��B
�� 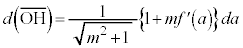
 �F
�F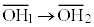 �̂Ƃ��Aa�F
�̂Ƃ��Aa�F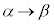 (
( ��a�ɂ��ĒP�������Ƃ�������ɂ��)
��a�ɂ��ĒP�������Ƃ�������ɂ��)
�� 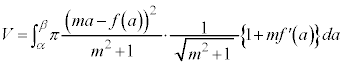
�@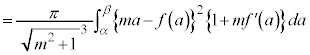
���D���ʂ̎��������Ƃ��ĈËL���Ă��Ӗ��͂���܂���B���ʂɎ��闬��𗝉����Ă��������B
��1�D�@��L�ɂ����āA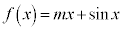 �C
�C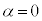 �C
�C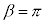 ���Ƃ��܂��B
���Ƃ��܂��B
���E��2�_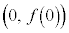 �C
�C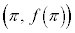 �́A
�́A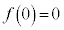 �C
�C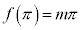 ���A�Ƃ��ɒ���
���A�Ƃ��ɒ���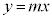 ��̓_�ł��B
��̓_�ł��B
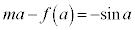
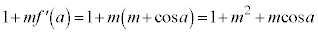
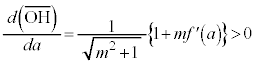 �͖�������Ă��܂��B����āA
�͖�������Ă��܂��B����āA
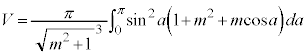
�@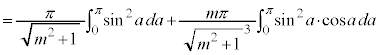
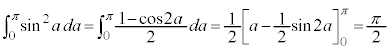
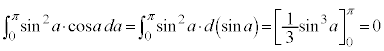
�� 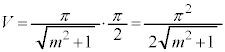
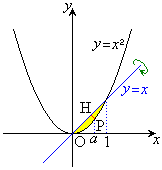 ��2�D�@������
��2�D�@������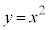 �ƒ���
�ƒ���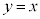 �ň͂܂��}�`��
�ň͂܂��}�`��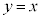 �̂܂���1��]���ē������]�̂̑̐ς����߂�B
�̂܂���1��]���ē������]�̂̑̐ς����߂�B
[��]�@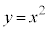 ��
��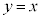 ��A������ƁA
��A������ƁA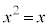 ���A
���A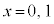
����āA������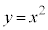 ��
��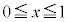 �̕�����
�̕�����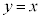 �̉���1��]���邱�ƂɂȂ�܂��B
�̉���1��]���邱�ƂɂȂ�܂��B
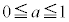 �Ƃ��āA������
�Ƃ��āA������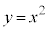 ��̓_P
��̓_P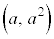 ��ʂ�A����
��ʂ�A����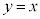 ����@�@�ɐ����Ȓ����́A
����@�@�ɐ����Ȓ����́A
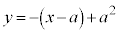 �@����A
�@����A
�@�C�A��A�����āA��_H��x���W�����߂�ƁA
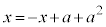
�� 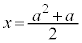 �@����B
�@����B
�_P�ƒ���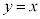 �Ƃ̋����́A
�Ƃ̋����́A
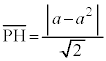
���_O��H�Ƃ̋����́A�B��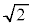 �{�ŁA
�{�ŁA
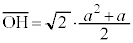 �@����C
�@����C
���߂�̐�V�́A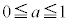 �̂Ƃ��A
�̂Ƃ��A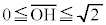 ���A
���A
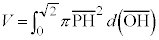
�C���ɂ��A�u���ϕ����܂��B�C����a�Ŕ������āA
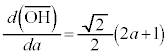
�� 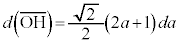
 �F
�F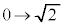 �̂Ƃ��Aa�F
�̂Ƃ��Aa�F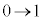
�� 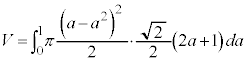
�@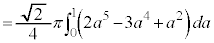
�@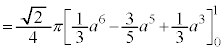
�@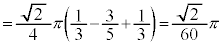 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 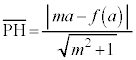
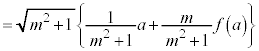
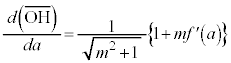
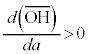 �Ƃ��܂��B�܂�A
�Ƃ��܂��B�܂�A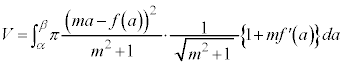
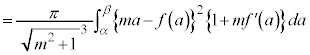
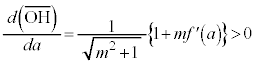 �͖�������Ă��܂��B����āA
�͖�������Ă��܂��B����āA