���H�吔�w'09�N�O��[2]
����a�ɑ��A����1���ϊ�
���l����B�ȉ���2�������݂�������L�����݂���悤��a�����߂�B
(1) L�͓_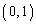 ��ʂ�B
��ʂ�B (2) �_Q��L��ɂ���A����f�ɂ�鑜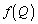 ��L��ɂ���B
��L��ɂ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�e97�N�̓����܂ŕp�o�ł������s�������̖��ł����A1���ϊ��̍s��\����^���ĕs�����������߂�A�Ƃ����̂ł͂Ȃ��A�s�������������������߂�A�Ƃ������ɂȂ��Ă��܂��B
(1)�̏������A����L���A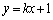 (k�͎����̒萔)�܂���
(k�͎����̒萔)�܂���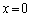 �ƕ\�����Ƃ��ł��܂��B
�ƕ\�����Ƃ��ł��܂��B
(i) ����L��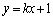 �̏ꍇ�A
�̏ꍇ�A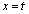 (t �͔C�ӂ̎���)�Ƃ��āA
(t �͔C�ӂ̎���)�Ƃ��āA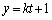
���܂�����L�F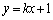 ��̓_�ɂȂ�̂ŁA
��̓_�ɂȂ�̂ŁA �������āA
t �͔C�ӂ̎����Ȃ̂ŁA
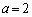 �Ƃ���ƁA
�Ƃ���ƁA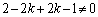 �Ȃ̂ŁA
�Ȃ̂ŁA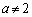
����āA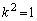 �C�܂�A
�C�܂�A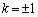 �ƂȂ�܂����A
�ƂȂ�܂����A
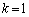 �Ƃ���ƁA
�Ƃ���ƁA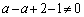 �Ȃ̂ŁA
�Ȃ̂ŁA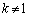
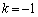 �Ƃ���ƁA
�Ƃ���ƁA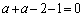
�� 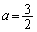 �@(���̂Ƃ��AL�F
�@(���̂Ƃ��AL�F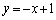 )
)(ii) ����L��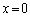 �̏ꍇ�A
�̏ꍇ�A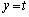 (t �͔C�ӂ̎���)�Ƃ��āA
(t �͔C�ӂ̎���)�Ƃ��āA ���܂�����L�F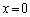 ��̓_�ɂȂ�̂ŁA
��̓_�ɂȂ�̂ŁA t �͔C�ӂ̎����Ȃ̂ŁA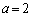 (i)�C(ii)���A
(i)�C(ii)���A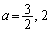 ......[��]
......[��] �NjL�D�s��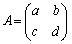 ���\��1���ϊ��ŁA�����F
���\��1���ϊ��ŁA�����F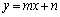 (
(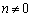 )�C�����F
)�C�����F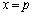 ��̓_���A�e�X�A���Ƃ̒�����Ɉڂ�������l���Ă݂܂��傤�B
��̓_���A�e�X�A���Ƃ̒�����Ɉڂ�������l���Ă݂܂��傤�B
�����F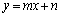 ��̓_�̍��W�́At�������Ƃ��āA
��̓_�̍��W�́At�������Ƃ��āA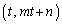 �Ƃ����܂��B
�Ƃ����܂��B
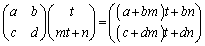 �@(���̏ꍇ��
�@(���̏ꍇ��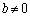 �Ƃ��܂�)
�Ƃ��܂�)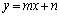 ��ɗ�������́A
��ɗ�������́A
t�ɂ��Đ������āA
t�Ɋւ�炸������������́A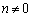 ���A
���A
b�������Đ�������ƁA
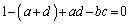 �@����@
�@����@
�ɂ����āA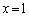 �Ƃ���
�Ƃ���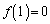 �ł����āAA���ŗL�l1�������Ƃ��Ӗ����Ă��܂��B
�ł����āAA���ŗL�l1�������Ƃ��Ӗ����Ă��܂��B
�����F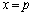 ��̓_�̍��W�́At�������Ƃ��āA
��̓_�̍��W�́At�������Ƃ��āA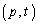 �������܂��B
�������܂��B
���A�ڂ�����̓_���Ăђ����F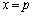 ��ɗ�������́A
��ɗ�������́A
t�ɂ��Đ������āA
t�Ɋւ�炸������������́A
(i) 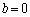 �C
�C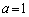 �̏ꍇ�͇@�Ɋ܂܂�܂��B�܂�AA���ŗL�l1�������܂��B
�̏ꍇ�͇@�Ɋ܂܂�܂��B�܂�AA���ŗL�l1�������܂��B (ii) 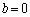 �C
�C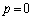 �̏ꍇ�́A
�̏ꍇ�́A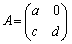 �̌`�ł���悢���ƂɂȂ�܂��B
�̌`�ł���悢���ƂɂȂ�܂��B (i)�́A�{��ł́A
�� 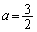
(ii)�́A�{��ł́AA��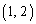 ����
����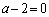 �Ƃ��āA
�Ƃ��āA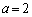
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B