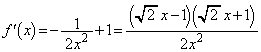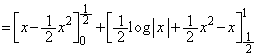���H�吔�w'11�N�O��[2]
����x�ɑ���
�Ƃ����B
(1) ��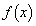 �̍ŏ��l�����߂�B
�̍ŏ��l�����߂�B (2) ��ϕ�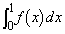 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ʓ|�Ȕ��ϕ��̖��Ɍ����܂����A�ꍇ�������邾���Ȃ̂ŁA���̖��͗��Ƃ��܂���B
(1) ��Βl���܂ޒ�ϕ��ł́A��Βl�L���̓����̐����Őϕ���Ԃ���K�v������܂��B
�Ƃ����܂��B
�ϕ����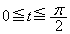 �ɂ�����
�ɂ�����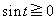 �C
�C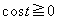 �ł��B
�ł��B (i) 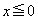 �̂Ƃ��A
�̂Ƃ��A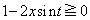
����āA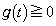 �C
�C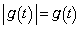
����āA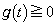 �C
�C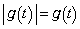
(iii) 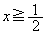 �̂Ƃ��A
�̂Ƃ��A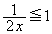
�ȏ���A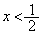 �̏ꍇ�ƁA
�̏ꍇ�ƁA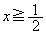 �̏ꍇ�ɕ����Đϕ��v�Z�����s���܂��B
�̏ꍇ�ɕ����Đϕ��v�Z�����s���܂��B �E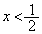 �̏ꍇ�A�܂�A(i)(ii)�̏ꍇ�A
�̏ꍇ�A�܂�A(i)(ii)�̏ꍇ�A 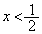 ���A
���A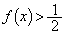 �@����@
�@����@�E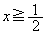 �̏ꍇ�A�܂�A(iii)�̏ꍇ�A
�̏ꍇ�A�܂�A(iii)�̏ꍇ�A 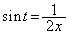 ����t��α�C
����t��α�C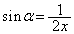 �Ƃ��āA(iii)(a)�ł�
�Ƃ��āA(iii)(a)�ł�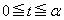 �C(iii)(b)�ł�
�C(iii)(b)�ł�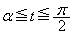 ���A
���A�����\���(���̑������Q��)�A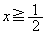 �ɂ����ẮA
�ɂ����ẮA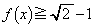 �@����A
�@����A �@�C�A���A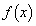 �̍ŏ��l��
�̍ŏ��l��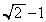 ......[��]�ʉ��D
......[��]�ʉ��D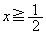 �̏ꍇ�ɂ��ẮA�������ϑ��敽�ς̊W��p���āA
�̏ꍇ�ɂ��ẮA�������ϑ��敽�ς̊W��p���āA 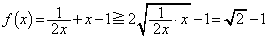 (�s�����̓��������́A
(�s�����̓��������́A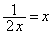 �C�܂�A
�C�܂�A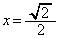 �̂Ƃ�)
�̂Ƃ�)�Ƃ��邱�Ƃ��ł��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B