三角関数の応用 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
(1) 2倍角の公式の応用
例1.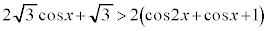 を解く。
を解く。
[解答] 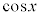 という項があるので、
という項があるので、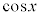 で統一して表します。
で統一して表します。
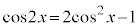 を代入すると、
を代入すると、
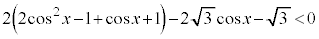
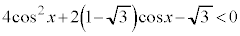
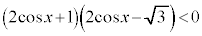
∴ 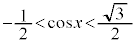
nを整数として、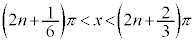 ,
,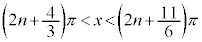 ......[答]
......[答]
例2.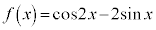 (
(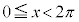 )の最大値と最小値
)の最大値と最小値
[解答] 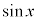 があるので、
があるので、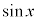 で統一して表します。
で統一して表します。
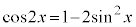 を代入すると、
を代入すると、
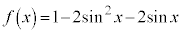
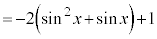
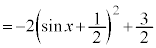
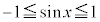 より、
より、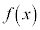 は、
は、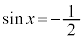 ,つまり、
,つまり、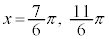 のときに、最大値:
のときに、最大値: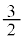
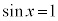 ,つまり、
,つまり、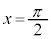 のときに、最小値:
のときに、最小値: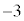
最大値: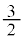 (
(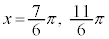 のとき),最小値:
のとき),最小値: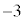 (
(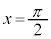 のとき) ......[答]
のとき) ......[答]
(2) 3倍角の公式の応用
例3.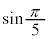 の値を求める。
の値を求める。
[解答] 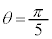 とすると、
とすると、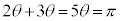 より、
より、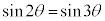
2倍角の公式、3倍角の公式より、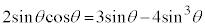
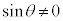 より、
より、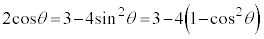
∴ 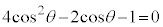
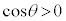 より、
より、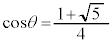
∴ 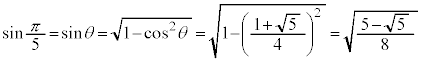 ......[答]
......[答]
例4.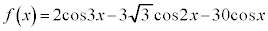 (
(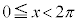 )の最大値と最小値
)の最大値と最小値
[解答] 3倍角の公式、2倍角の公式より、
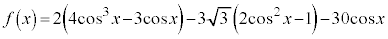
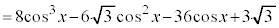
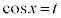 とおくと、
とおくと、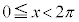 のとき、
のとき、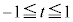
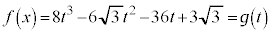 とおきます。
とおきます。
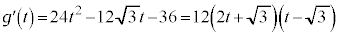
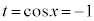 のとき、
のとき、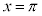 ,
,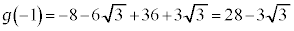
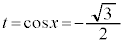 のとき、
のとき、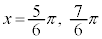 ,
,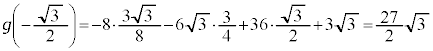
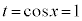 のとき、
のとき、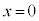 ,
,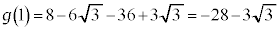
増減表より、最大値: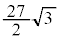 (
(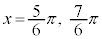 のとき),最小値:
のとき),最小値: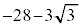 (
(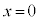 のとき) ......[答]
のとき) ......[答]
(3) 和積の公式の応用
例5.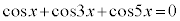 (
(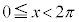 )を解く。
)を解く。
[解答] 和積の公式より、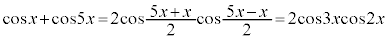
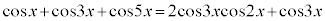
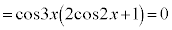
∴ 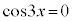 または
または 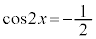
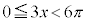 より、
より、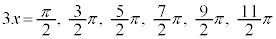
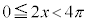 より、
より、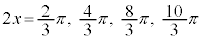
∴ 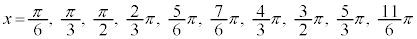 ......[答]
......[答]
例6.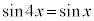 (
(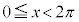 )を解く。
)を解く。
[解答] 和積の公式より、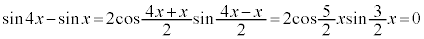
∴ 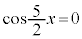 または
または 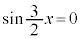
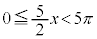 より、
より、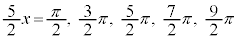
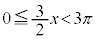 より、
より、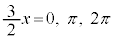
∴ 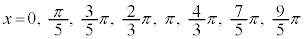 ......[答]
......[答]
注.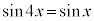 より直ちに
より直ちに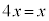 としてしまうと、
としてしまうと、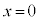 以外の解が得られなくなってしまいます。
以外の解が得られなくなってしまいます。
(4) 積和の公式の応用
例7.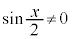 のとき、
のとき、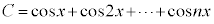 ,
,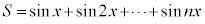 (n:自然数)
(n:自然数)
[解答] 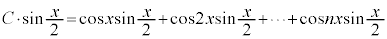
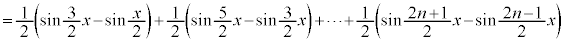
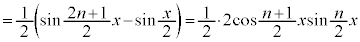
∴ 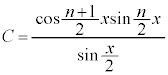 ......[答]
......[答]
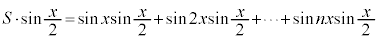
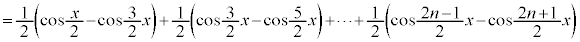
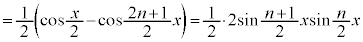
∴ 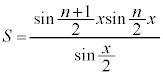 ......[答]
......[答]
例8.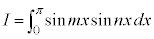 (m,nは自然数)
(m,nは自然数)
[解答] 積和の公式より、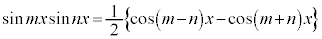
よって、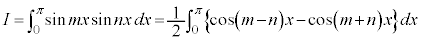
ここで、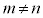 のときには、
のときには、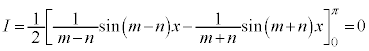
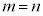 のときには、
のときには、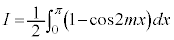
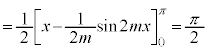
以上より、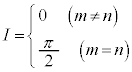
(5) 合成の応用
例9.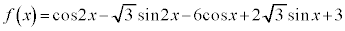 (
(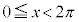 )の最大値と最小値
)の最大値と最小値
[解答] 2倍角の公式を用いて、
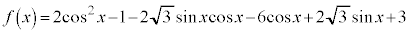
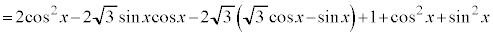
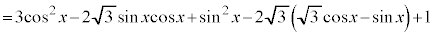
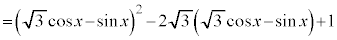
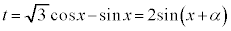 とおくと、
とおくと、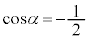 ,
,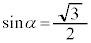 より、
より、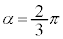 (三角関数の合成を参照)
(三角関数の合成を参照)
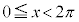 において、
において、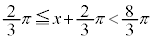 ,
,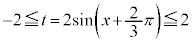
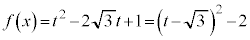
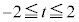 より、
より、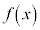 は、
は、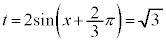 ,つまり、
,つまり、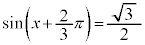 ,
,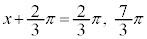 ,
,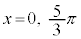 のときに、最小値:
のときに、最小値: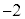 をとります。
をとります。
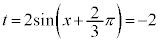 ,つまり、
,つまり、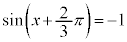 ,
,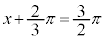 ,
,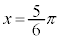 のときに、最大値:
のときに、最大値: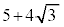 をとります。
をとります。
よって、最大値: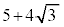 (
(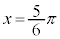 のとき),最小値:
のとき),最小値: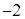 (
(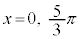 のとき) ......[答]
のとき) ......[答]
(6) 図形的解法
例10.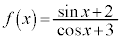 の最大値と最小値
の最大値と最小値
[解答] 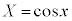 ,
,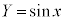 とおくと、
とおくと、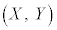 は単位円上の点です。
は単位円上の点です。
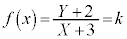 とおくと、
とおくと、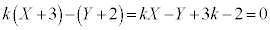 は、定点
は、定点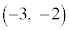 を通る直線になっています。
を通る直線になっています。
単位円と直線が共有点をもつのは、円の中心と直線との距離: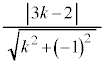 が、円の半径1以下であることです。
が、円の半径1以下であることです。
∴ 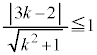
分母を払って2乗すると、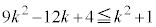
∴ 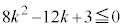
∴ 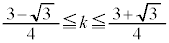
よって、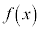 の最大値:
の最大値: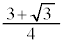 ,最小値:
,最小値: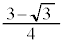 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 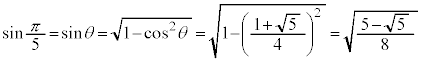 ......[答]
......[答]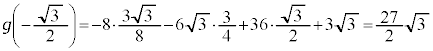
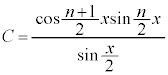 ......[答]
......[答]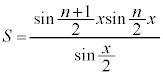 ......[答]
......[答]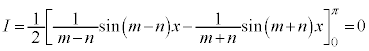
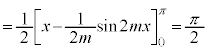
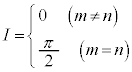
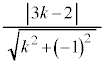 が、円の半径1以下であることです。
が、円の半径1以下であることです。