三角形の条件 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
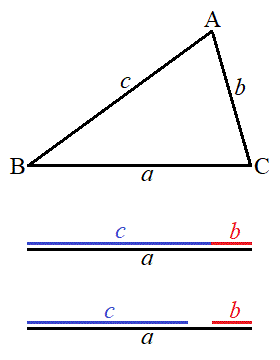 3辺がa,b,cの三角形について、
3辺がa,b,cの三角形について、
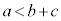 かつ
かつ 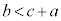 かつ
かつ 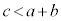 (三角形の2辺の和は他の1辺より大) ・・・①
(三角形の2辺の和は他の1辺より大) ・・・①
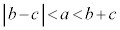 ・・・②
・・・②
条件①と条件②は同値。
また、a,b,cに向かい合う角をA,B,Cとすると、a,b,cの大小関係とA,B,Cの大小関係は一致する。
三角形の3辺の長さがa,b,cと与えられたときに、三角形ができるための条件が①または②です。
仮に、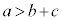 になってしまうと、右上図のように、三角形ができません。
になってしまうと、右上図のように、三角形ができません。
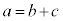 であっても、三角形はできません。
であっても、三角形はできません。
少なくとも、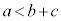 であることが必要です。同様にして、
であることが必要です。同様にして、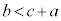 ,
,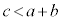 が必要です。逆に、①であれば、3辺の長さがa,b,cの三角形ができます。
が必要です。逆に、①であれば、3辺の長さがa,b,cの三角形ができます。
①の2番目の式と、3番目の式を移項すると、
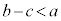 ,
,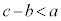
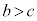 と
と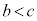 の場合をまとめて、
の場合をまとめて、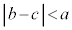
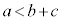 と合わせて、
と合わせて、
よって、① ⇔ ② です。
また、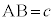 ,
,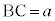 ,
,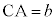 である三角形ABCの外接円の半径をRとして、正弦定理より、
である三角形ABCの外接円の半径をRとして、正弦定理より、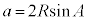 ,
,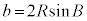
ここで、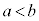 ,即ち、
,即ち、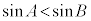 だとすると、
だとすると、
・A,Bともに鋭角の場合、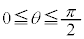 において
において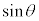 は単調増加なので、
は単調増加なので、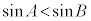 なら
なら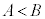 です。
です。 ・Aが直角または鈍角のとき、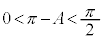 ,
,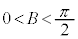 ,
,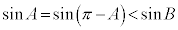 より、
より、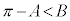 で
で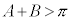 となってしまうので、不適。
となってしまうので、不適。 ・Bが直角または鈍角ならば、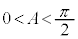 なので、
なので、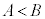 です。
です。 以上より、大きい辺に向かい合う角は小さい辺に向かい合う角よりも大きくなります。つまり、辺の大小関係と向かい合う角の大小関係は一致します。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。