三角関数のグラフ 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目の内容については、三角関数も参照してください。
実数xに対して、関数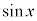 の値は、xを一般角として、単位円(原点を中心とする半径1の円)の円周上をx軸から反時計回りにxだけ回った点のy座標です。
の値は、xを一般角として、単位円(原点を中心とする半径1の円)の円周上をx軸から反時計回りにxだけ回った点のy座標です。
 従って、
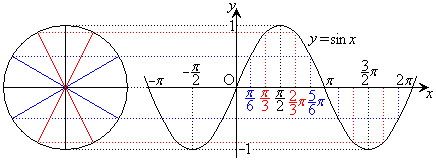
従って、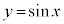 のグラフを書くためには、右図のように、単位円の1つの直径の延長上にx軸を引いておき、円周上で直径から弧度法で測った角xだけ回った点を通りx軸に平行な直線を伸ばして、この直線上でx座標がxのところに点をとり、こうして得られる点を結んでいきます。
のグラフを書くためには、右図のように、単位円の1つの直径の延長上にx軸を引いておき、円周上で直径から弧度法で測った角xだけ回った点を通りx軸に平行な直線を伸ばして、この直線上でx座標がxのところに点をとり、こうして得られる点を結んでいきます。
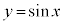 のグラフは波動の状況をあらすグラフになっています。
のグラフは波動の状況をあらすグラフになっています。
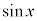 には、nを整数として、
には、nを整数として、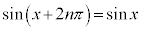 という性質があるので、
という性質があるので、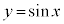 のグラフは、x座標が
のグラフは、x座標が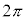 進むごとに同じ形になります。
進むごとに同じ形になります。
このように、xがある決まった値pだけ変化するたびにy座標が等しくなるような関数を周期関数と言い、pを周期と言います。
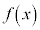 が周期pの周期関数であるとき、
が周期pの周期関数であるとき、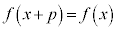 が成り立ちます。
が成り立ちます。
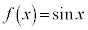 だとすると、
だとすると、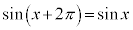 より
より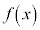 は周期
は周期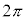 の周期関数なので、
の周期関数なので、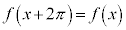 となります。
となります。
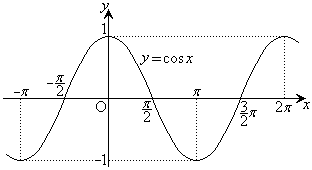
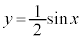 のグラフは、右図のように、
のグラフは、右図のように、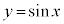 のグラフ上の各点において、y座標の値を
のグラフ上の各点において、y座標の値を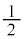 にした点をつなぐことにより得られます。
にした点をつなぐことにより得られます。
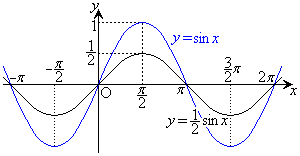
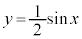 のグラフと
のグラフと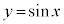 のグラフを比較すると、波動の振れが
のグラフを比較すると、波動の振れが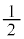 になっています。
になっています。
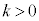 として、
として、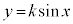 のグラフは、
のグラフは、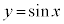 の波動の振れをk倍にしたグラフになります。このkの値を振幅と言います。
の波動の振れをk倍にしたグラフになります。このkの値を振幅と言います。
関数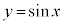 の振幅は1,関数
の振幅は1,関数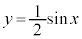 の振幅は
の振幅は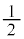 です。
です。
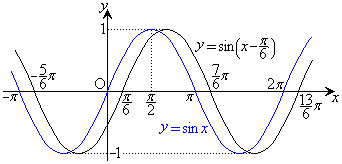
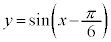 のグラフは、右図のように、
のグラフは、右図のように、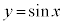 のグラフをx軸正方向に
のグラフをx軸正方向に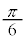 だけ平行移動したものになります(平行移動については、2次関数でも考えました。2次関数を参照)。
だけ平行移動したものになります(平行移動については、2次関数でも考えました。2次関数を参照)。
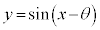 のグラフは、
のグラフは、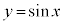 のグラフをx軸正方向にθ だけ平行移動させたグラフです。
のグラフをx軸正方向にθ だけ平行移動させたグラフです。
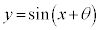 のグラフは、
のグラフは、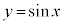 のグラフをx軸負方向にθ だけ平行移動させたグラフです。
のグラフをx軸負方向にθ だけ平行移動させたグラフです。
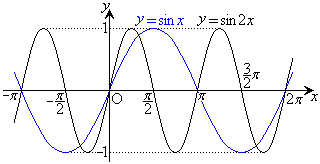
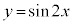 のグラフは、
のグラフは、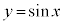 のグラフと比較すると、右図のように左右に2倍に押し縮められたようなグラフになります。周期はπになります。
のグラフと比較すると、右図のように左右に2倍に押し縮められたようなグラフになります。周期はπになります。
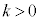 として、
として、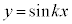 のグラフの周期は、
のグラフの周期は、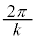 となります。
となります。
なぜなら、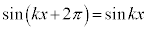 より、
より、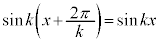 ,つまり、
,つまり、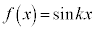 として、
として、 が成り立つからです。
が成り立つからです。
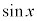 と
と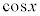 の間には、
の間には、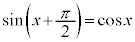 という関係があるので、
という関係があるので、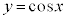 のグラフは、
のグラフは、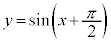 のグラフと同じグラフであり、
のグラフと同じグラフであり、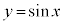 のグラフをx軸負方向に
のグラフをx軸負方向に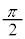 だけ平行移動させたものになります。
だけ平行移動させたものになります。
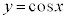 も
も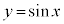 と同様に周期
と同様に周期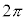 の周期関数です。
の周期関数です。
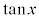 は、
は、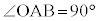 (
(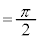 )である直角三角形OABにおいて、
)である直角三角形OABにおいて、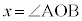 (xは弧度法で測った角)として、
(xは弧度法で測った角)として、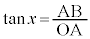 なので、OAの長さを1としておけば、ABの長さが
なので、OAの長さを1としておけば、ABの長さが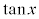 の値になります(
の値になります(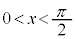 )。
)。
従って、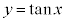 のグラフを書くためには以下のようにします。
のグラフを書くためには以下のようにします。
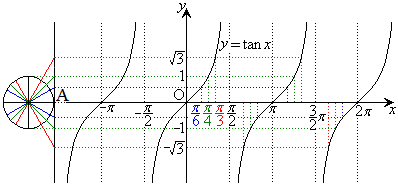 右図のように、単位円の1つの直径の延長上にx軸を引いておき、この直径のx軸側の端点をAとして、点Aにおける円の接線を引きます。単位円の円周上をこの直径からxだけ回った点と円の中心を直線で結びます。この直線と先の接線との交点を通ってx軸に平行な直線を引きます。この平行線上でx座標がxとなるところに点をとり、こうして得られる点を結んでいけば、
右図のように、単位円の1つの直径の延長上にx軸を引いておき、この直径のx軸側の端点をAとして、点Aにおける円の接線を引きます。単位円の円周上をこの直径からxだけ回った点と円の中心を直線で結びます。この直線と先の接線との交点を通ってx軸に平行な直線を引きます。この平行線上でx座標がxとなるところに点をとり、こうして得られる点を結んでいけば、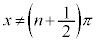 (nは整数)に対して、
(nは整数)に対して、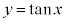 のグラフを書くことができます。
のグラフを書くことができます。
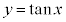 のグラフは、x座標がπ進むごとに同じ形が繰り返されていきます。
のグラフは、x座標がπ進むごとに同じ形が繰り返されていきます。
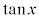 については、
については、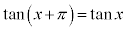 という性質があるので、
という性質があるので、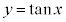 は周期πの周期関数です。
は周期πの周期関数です。
また、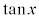 の値は、nを整数として、
の値は、nを整数として、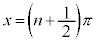 のときには定義できません。
のときには定義できません。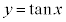 のグラフは、xが
のグラフは、xが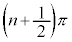 に近づくと、x軸から急速に離れていき、x軸に垂直な直線
に近づくと、x軸から急速に離れていき、x軸に垂直な直線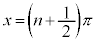 に近づいていきます。従って、
に近づいていきます。従って、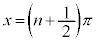 は
は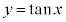 のグラフの漸近線になっています。
のグラフの漸近線になっています。
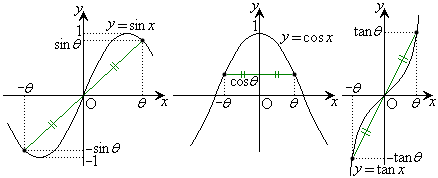
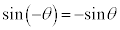 という性質により、点
という性質により、点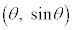 と点
と点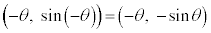 は原点に関して対称です。従って、
は原点に関して対称です。従って、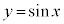 のグラフは、右図のように、原点に関して対称になります。よって、
のグラフは、右図のように、原点に関して対称になります。よって、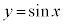 は奇関数です。
は奇関数です。
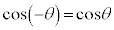 という性質により、点
という性質により、点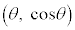 と点
と点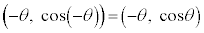 はy軸に関して対称です。従って、
はy軸に関して対称です。従って、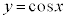 のグラフは、右図のようにy軸に関して対称になります。よって、
のグラフは、右図のようにy軸に関して対称になります。よって、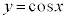 は偶関数です。
は偶関数です。
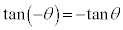 という性質により、点
という性質により、点 と点
と点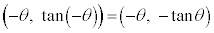 は原点に関して対称です。従って、
は原点に関して対称です。従って、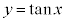 のグラフは、右図のように、原点に関して対称になります。よって、
のグラフは、右図のように、原点に関して対称になります。よって、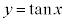 は奇関数です。
は奇関数です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。